Problema
(Indicado a partir do 9º ano do E. F.)
Duas velas têm formatos cilíndricos, mas comprimentos e diâmetros diferentes. Depois de acesas, a mais longa queimou totalmente em 7 horas e a menor, em 10 horas.
Sabendo que, após queimarem juntas durante 4 horas, elas ficaram com o mesmo comprimento, qual a razão entre os comprimentos iniciais da menor e da maior vela?
 Imagem adaptada de Freepik.com
Imagem adaptada de Freepik.com
Solução 1
Sejam [tex]l_1[/tex] e [tex]l_2[/tex] os comprimentos iniciais das velas, com [tex]l_1 > l_2[/tex].
Vamos supor que o material das velas é uniforme; logo, a velocidade de queima é constante ao longo do experimento.
Assim, considerando as velocidades de queima em comprimento por hora, temos que [tex]v_1 = \dfrac{l_1}{7}[/tex] e [tex]v_2 = \dfrac{l_2}{10}[/tex].
Após quatro horas, o comprimento consumido na maior vela será [tex]v_1 \cdot 4[/tex] e, na menor vela, [tex]v_2 \cdot 4[/tex]. Como as duas velas ficaram com o mesmo comprimento, segue que:
[tex]\qquad l_1-v_1 \cdot 4 = l_2-v_2 \cdot 4\\
\qquad l_1-\dfrac{l_1}{7}\cdot 4 = l_2-\dfrac{l_2}{10} \cdot 4\\
\qquad \dfrac{3\,l_1}{7} =\dfrac{6\,l_2}{10}\\
\qquad \dfrac{l_2}{l_1} = \dfrac{5}{7}\,.[/tex]
Assim, a razão entre os comprimentos iniciais da menor e da maior vela é [tex]\,\fcolorbox{black}{#eee0e5}{$\dfrac{5}{7}$}[/tex] .
Solução elaborada pelos Moderadores do Blog.
Solução 2
Sejam [tex]h_1[/tex] e [tex]h_2[/tex] os comprimentos iniciais das velas, com [tex]h_1 > h_2[/tex].
Pelas informações do problema, a vela mais longa queimou totalmente em [tex]7[/tex] horas e a outra queimou em [tex]10[/tex] horas. Assim, a cada hora, a vela mais alta perde [tex]1/7[/tex] de sua altura e, a outra, [tex]1/10[/tex]; ou seja, [tex]\dfrac{h_1}{7}[/tex] e [tex]\dfrac{h_2}{10}[/tex] respectivamente.
- Com isso, após queimarem juntas por quatro horas:
- a mais longa perdeu [tex]4 \times \dfrac{h_1}{7}= \dfrac{4h_1}{7}[/tex] da sua altura e, portanto, ficou com
[tex] \qquad h_1-\dfrac{4h_1}{7}=\boxed{\dfrac{3h_1}{7}}[/tex] de altura; - a mais curta perdeu [tex]4 \times \dfrac{h_2}{10}= \dfrac{4h_2}{10}[/tex] da sua altura e, portanto, ficou com
[tex] \qquad h_2-\dfrac{4h_2}{10}=\boxed{\dfrac{6h_2}{10}}[/tex] de altura.
Observem a figura abaixo.
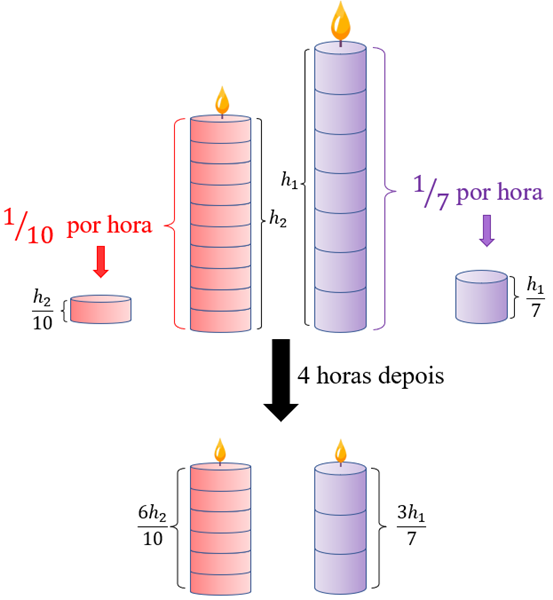
Mas após queimarem por quatro horas, essas alturas são iguais; logo temos que:
[tex]~~\\
\qquad \dfrac{3h_1}{7}=\dfrac{6h_2}{10}\\
\qquad \dfrac{3h_1}{7}=\dfrac{3h_2}{5}\\
\qquad \dfrac{h_1}{7}=\dfrac{h_2}{5}\\
\qquad \dfrac{h_2}{5}= \dfrac{h_1}{7}\\
\qquad \dfrac{h_2}{h_1} = \dfrac{5}{7}\,.[/tex]
Assim, a razão entre os comprimentos iniciais da menor e da maior vela é [tex]\,\fcolorbox{black}{#eee0e5}{$\dfrac{5}{7}$}[/tex] .
Solução elaborada pelos Moderadores do Blog.
