.Problemão: Somando distâncias

Problema
(Indicado a partir do 9º ano do E. F.)

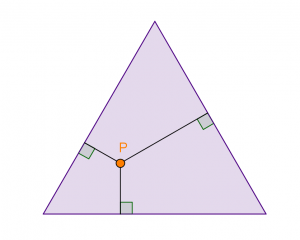
Seja [tex]P[/tex] um ponto no interior de um triângulo equilátero qualquer.
Prove que a soma das distâncias de [tex]P[/tex] aos lados desse triângulo é sempre constante.
Interprete geometricamente o valor desta constante.

Solução

Sejam [tex]h_1[/tex], [tex]h_2[/tex] e [tex]h_3[/tex] as distâncias de [tex]P[/tex] aos lados do triângulo dado.

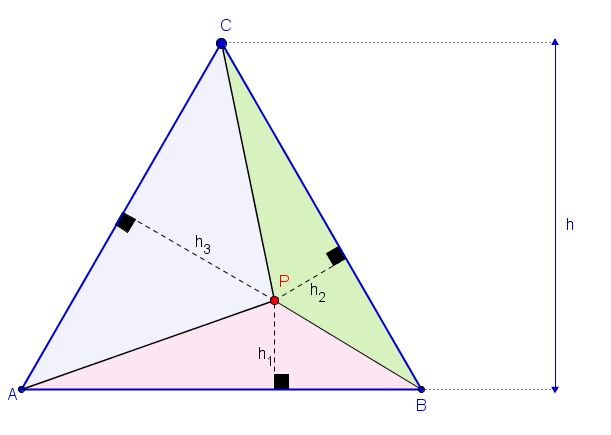
• Note que a área do triângulo é dada por [tex]\dfrac{l \cdot h} {2}[/tex], sendo [tex]l[/tex] a base (o comprimento de qualquer um dos lados, já que o triângulo é equilátero) e [tex]h[/tex] é a altura relativa ao lado escolhido (a altura [tex]h[/tex] é sempre a mesma, independente do lado, pois o triângulo é equilátero).
• Por outro lado, observamos que a área do triângulo também pode ser obtida como a soma das áreas dos três triângulos, cujas alturas são [tex]h_1[/tex], [tex]h_2[/tex] e [tex]h_3[/tex] e as bases são [tex]l[/tex].

Assim, temos que
[tex]\qquad Área=\dfrac{l \cdot h} {2} = \dfrac{l \cdot h_1} {2} + \dfrac{l \cdot h_2} {2} + \dfrac{l \cdot h_3} {2} = \dfrac{l \cdot (h_1+h_2+h_3)} {2}[/tex],
donde
[tex]\qquad \fbox{$\displaystyle h_1+h_2+h_3 =h$}[/tex] .
Portanto, a soma das distâncias de [tex]P[/tex] aos lados do triângulo é sempre constante e igual à altura do triângulo equilátero dado.

Solução elaborada pelos Moderadores do Blog.

Testando a solução

Você pode utilizar o applet disponibilizado abaixo para simular diferentes condições iniciais para o problema e, com isso, observar a veracidade da afirmação demonstrada, quantas vezes você quiser!
Para tanto, carregue o applet, escolha um triângulo equilátero e modifique a posição do ponto P.