Problema
(Indicado a partir do 9º ano do E. F.)
(Adaptado de FUVEST) Os pontos [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] são colineares, [tex]AB = 5[/tex], [tex]BC = 2[/tex] e [tex]B[/tex] está entre [tex]A[/tex] e [tex]C[/tex]. Os pontos [tex]C[/tex] e [tex]D[/tex] pertencem a uma circunferência com centro em [tex]A[/tex]. Traça-se uma reta [tex]r[/tex] perpendicular ao segmento [tex]\overline{BD}[/tex] passando pelo seu ponto médio. Chama-se de [tex]P[/tex] a intersecção de [tex]r[/tex] com [tex]\overline{AD}[/tex].
Calcule o valor de [tex]AP + BP.[/tex]

Lembretes e notações
(I) Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex].
(II) Denotaremos o comprimento do segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]XY[/tex].
Solução
Considere a figura, em que [tex]M[/tex] é o ponto médio de [tex]\overline{BD}[/tex].
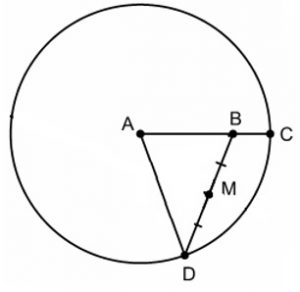
Note que a reta [tex]r[/tex] do enunciado é a mediatriz do triângulo [tex]ABC[/tex] relativa ao lado [tex]\overline{BD}[/tex] e que a circunferência possui raio [tex]AB + BC = 5 + 2 = 7[/tex].
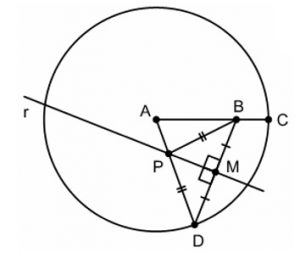
Como o ponto [tex]P[/tex] pertence à mediatriz, temos que [tex]PB[/tex] = [tex]PD[/tex].
Assim, [tex]AP + PD = AP + PB[/tex]. Como [tex]AP + PD[/tex] é o raio da circunferência, [tex]AP + PB = 7[/tex].
Solução elaborada pelos Moderadores do Blog.
