✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 9º ano do E. F.)
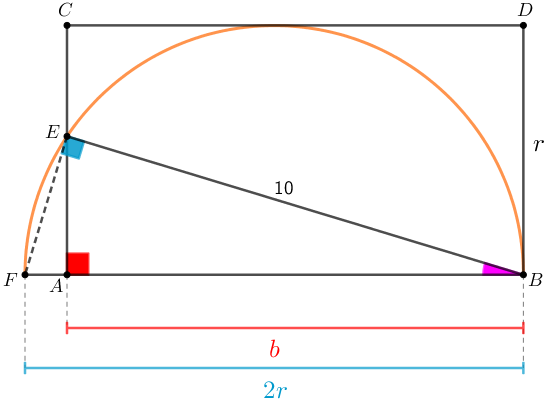
Na figura temos um retângulo [tex]ABDC[/tex] e um semicírculo de diâmetro [tex]\overline{FB}[/tex].
Sabendo que o lado [tex]\overline{DC}[/tex] é tangente ao semicírculo e que o comprimento da corda [tex]\overline{BE}[/tex] vale [tex]10[/tex], calcule a área do retângulo.
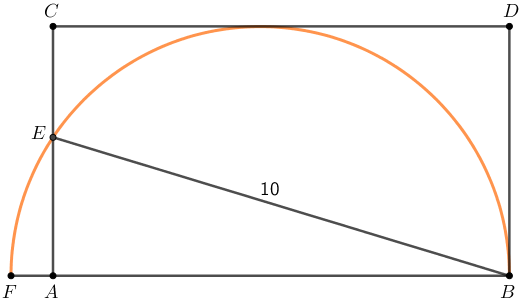
Adaptado de Aman’s Math Blog.

Lembretes
(I) Se um triângulo está inscrito em uma circunferência (ou semicircunferência) e um de seus lados é um diâmetro, então esse triângulo é retângulo e o diâmetro é a sua hipotenusa;
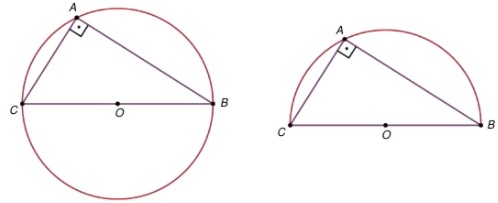
(II) Caso de semelhança A.A. (ângulo – ângulo): Se dois ângulos de um triângulo são congruentes (têm o mesmo tamanho) a dois ângulos de outro triângulo, então estes triângulos são semelhantes (para aprender mais, visite a Sala para leitura Um pouco sobre semelhança de triângulos).
Solução
Inicialmente, vamos construir o segmento [tex]\overline{FE}[/tex] e analisar o triângulo [tex]FEB[/tex].
- Pelo Lembrete (I), temos que o triângulo [tex]FEB[/tex] é retângulo, sendo [tex]\hat E[/tex] o seu ângulo reto.
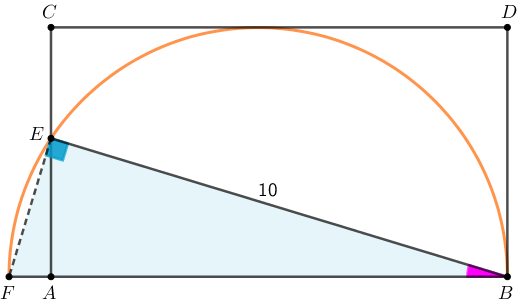
- Por outro lado, [tex]ABDC[/tex] é um retângulo; logo, o triângulo [tex]EAB[/tex] também é retângulo, sendo [tex]\hat A[/tex] o seu ângulo reto.
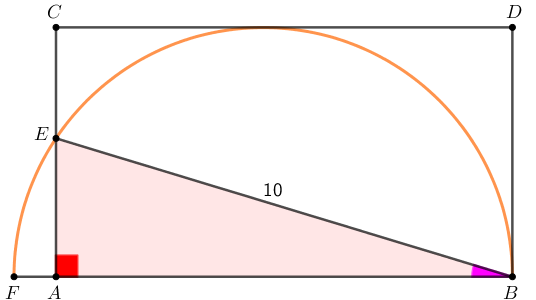
- Agora, observe que o vértice [tex]B[/tex] é comum aos dois triângulos.
Assim, pelo exposto e usando o Lembrete (II), podemos concluir que os triângulos [tex]FEB[/tex] e [tex]EAB[/tex] são semelhantes.
Finalmente, para o cálculo da área do retângulo [tex]ABDC[/tex], note que:
- a área de um retângulo qualquer é calculada pela multiplicação do comprimento da base pelo comprimento da altura;
- o comprimento da altura do retângulo [tex]ABDC[/tex] é igual ao comprimento do raio da semicircunferência;
- pela semelhança dos triângulos [tex]FEB[/tex] e [tex]EAB[/tex], se [tex]b[/tex] é o comprimento da base do retângulo segue que [tex]\boxed{\dfrac{10}{2R}=\dfrac{b}{10}}.[/tex]
Portanto, [tex]b \cdot R=\dfrac{100}{2}=50[/tex], ou seja, [tex]\,\fcolorbox{black}{#eee0e5}{$Área_{ABDC}=50$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
