Problema
(Indicado a partir do 1º ano do E. M.)
Na cidade de Geometrix há quatro bairros muito conhecidos: Pitágoras, Euler, Tales e Gauss.
Parte do mapa dessa cidade mostra o alinhamento de três dos referidos bairros e mostra também que todos estão localizados em um quadrado de lado [tex]10[/tex] km, sendo que Pitágoras está no meio do lado desse quadrado.
Com o objetivo de melhorar o transporte entre as localidades da cidade, a prefeitura quer construir uma avenida ligando os três bairros colineares e uma outra avenida ligando Euler a Gauss de forma que a avenida Euler-Gauss seja perpendicular ao lado do quadrado que passa por Gauss.
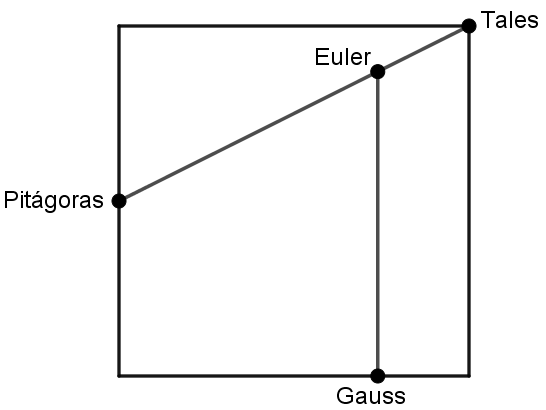
Sabe-se que o trecho que ligará Pitágoras a Euler medirá o quádruplo da distância entre os bairros Euler e Tales. Qual a extensão da avenida Euler-Gauss?

Ajuda
(1) Teorema Fundamental da Proporcionalidade:
Se uma reta paralela a um dos lados de um triângulo intersecta os outros dois lados em pontos distintos, então essa reta determina um triângulo semelhante ao triângulo inicial. (Para conhecer um pouco mais sobre esse resultado, clique AQUI.)
(2) Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X \, [/tex] e [tex] \, Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY[/tex].
Solução
A partir da figura fornecida no problema, vamos prolongar o segmento que representa a avenida ligando Euler a Gauss e obtemos, então, a figura a seguir, na qual o ponto [tex]D[/tex] é a interseção do prolongamento que fizemos com o lado [tex]\overline{AT}[/tex].
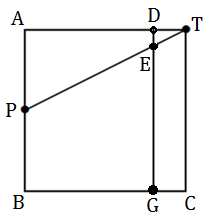
- Uma vez que [tex]\overline{EG}[/tex] é perpendicular a [tex]\overline{BC}[/tex], temos [tex]\overline{DG}\parallel \overline{AB}[/tex], donde [tex]\overline{DE}\parallel \overline{AP}[/tex]. Assim, os triângulos [tex]TDE[/tex] e [tex]TAP[/tex] são semelhantes. (Veja a Ajuda.)
Da semelhança entre os triângulos [tex]TDE[/tex] e [tex]TAP[/tex], temos que [tex]\dfrac{DE}{AP}=\dfrac{TE}{TP}. \qquad \textcolor{#800000}{(i)}[/tex] - Por outro lado, o trecho que ligará Pitágoras a Euler medirá o quádruplo da distância entre os bairros Euler e Tales. Logo, se essa distância em quilômetros for [tex]d[/tex], segue que:
– o comprimento de [tex]\overline{TE}[/tex] é [tex]d[/tex];
– o comprimento de [tex]\overline{EP}[/tex] é [tex]4d[/tex];
– o comprimento de [tex]\overline{TP}[/tex] é [tex]5d[/tex].
Assim, segue de [tex] \textcolor{#800000}{(i)}[/tex] que:
[tex]\qquad \qquad \dfrac{DE}{AP}=\dfrac{TE}{TP}\\
\qquad \qquad \dfrac{DE}{AP}=\dfrac{\cancel{d}}{5\cancel{d}}\\
\qquad \qquad \dfrac{DE}{5}=\dfrac{1}{5}\\
\qquad \qquad DE=\dfrac{1}{5} \cdot 5=1 \, km \, .[/tex]
Portanto, a extensão da avenida Euler-Gauss será [tex] \, \fcolorbox{black}{#eee0e5}{$10\ km – 1\ km = 9\ km$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
