Problema
(Indicado a partir do 3º ano do E. M.)
O poliedro convexo da imagem abaixo é chamado de rombicosidodecaedro.
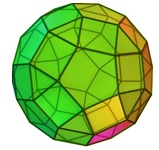
Esse sólido é formado por [tex]62[/tex] faces, todas polígonos regulares. Cada vértice desse poliedro é um vértice em comum de dois quadrados, um triângulo e um pentágono.
Qual o número de faces quadradas, triangulares e pentagonais do rombicosidodecaedro?
Extraído de FGV.

Lembrete e notação
Relação de Euler:
Seja [tex]V[/tex] o número de vértices, [tex]F[/tex] o número de faces e [tex]A[/tex] o número de arestas de um poliedro convexo. Então: [tex]V+F=A+2[/tex].
Solução
Como em cada vértice concorrem [tex]4[/tex] arestas, poderíamos pensar que [tex]A=4V[/tex]. Porém, cada aresta concorre em dois vértices distintos. Assim, podemos escrever
[tex]\qquad A=\dfrac{4V}{2}=2V.[/tex]
Pela relação de Euler, temos:
[tex]\qquad V+F=A+2,[/tex]
[tex]\qquad V+62=2V+2,[/tex]
[tex]\qquad V=60.[/tex]
Como cada vértice pertence a exatamente uma face triangular, o número de faces triangulares, [tex]F_{3}[/tex], é dado por
[tex]\qquad F_{3}=\dfrac {60}{3}=20. [/tex]
De modo análogo, o número de faces pentagonais, [tex]F_{5}[/tex], é
[tex]\qquad F_{5}=\dfrac {60}{5}=12.[/tex]
Como há [tex]62[/tex] faces, teremos [tex]F_{4}=62-32=30[/tex] faces quadradas.
Solução elaborada pelos Moderadores do Blog.
