.Problema: Quais são os algarismos?

Problema
(Indicado a partir do 8º ano do E. F.)

---

Com os algarismos [tex]x [/tex], [tex]y[/tex] e [tex]z[/tex], formam-se os números de dois algarismos [tex]x\,y\,[/tex] e [tex]\,y\,x[/tex] cuja soma é o número de três algarismos [tex]z\,x\,z[/tex].
Quais são os algarismos [tex]x[/tex], [tex]\,y \,[/tex] e [tex]\,z\, [/tex]?

---

Observação: Neste problema, denotaremos por [tex]\,a\,b\,c\,\,[/tex] a representação decimal do número de três algarismos cujos algarismos das centenas, dezenas e unidades são [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex], respectivamente.
Assim, [tex] a\,b\,c=100\cdot a + 10\cdot b + c[/tex].
De maneira análoga, a representação decimal do número de dois algarismos cujos algarismos das dezenas e unidades são [tex]a[/tex] e [tex]b[/tex], respectivamente, será [tex] a\,b[/tex] e, portanto, [tex] a\,b=10\cdot a+b[/tex].

Solução

---

Inicialmente, observe que:
[tex]\quad \textcolor{#0DC0FF}{\rhd}\,[/tex] como o número [tex]x\,y\,[/tex] tem dois algarismos, então [tex]x\ne 0[/tex];
[tex]\quad \textcolor{#0DC0FF}{\rhd}\,[/tex] como o número [tex]y\,x\,[/tex] tem dois algarismos, então [tex]y\ne 0[/tex];
[tex]\quad \textcolor{#0DC0FF}{\rhd}\,[/tex] como o número [tex]z\,x\,z\,[/tex] tem três algarismos, então [tex]z\ne 0[/tex].
Assim, [tex]x [/tex], [tex]y[/tex] e [tex]z [/tex] são algarismos não nulos, isto é, são números naturais tais que [tex]0 \lt x\,,\,y\,,\, z \le 9[/tex].
Observe, também, que:
[tex]\quad \textcolor{#0DC0FF}{\rhd}\,[/tex] o maior número que pode ser formado somando dois números de dois algarismos é [tex]198=99+99[/tex].
Logo, como [tex]x\,y+y\,x=z\,x\,z[/tex], então [tex]z\,x\,z[/tex] é um número de três algarismos resultante da soma de dois números com dois algarismos cada. Dessa forma,
[tex]\qquad \qquad \textcolor{red}{1}00 \le \textcolor{red}{z}\,x\,z \le \textcolor{red}{1}98[/tex]
e, portanto, concluímos que [tex]\boxed{\textcolor{red}{z=1}}[/tex].
Como [tex]z=1[/tex], o resultado da soma é [tex]1\,x\,1[/tex] e, desse modo, segue que:
[tex]\qquad x\,y +y\,x =1\,x\,1[/tex]
[tex]\qquad (10\cdot x + y) + (10\cdot y + x) = 100 + 10\cdot x + 1 [/tex]
[tex]\qquad 11\cdot y + x = 101[/tex].
Respeitando as condições do problema, esta equação só admite a solução [tex]\boxed{x=2}[/tex] e [tex]\boxed{y=9}[/tex].
Assim, [tex] \,\fcolorbox{black}{#eee0e5}{$x=2$}\,\,[/tex], [tex] \,\fcolorbox{black}{#eee0e5}{$y=9$}\,\,[/tex] e [tex] \,\,\fcolorbox{black}{#eee0e5}{$z=1$}\,.[/tex]

---

---

Você pode verificar a afirmação de que a equação [tex]\boxed{11\cdot y + x = 101}[/tex] só admite a solução [tex]\boxed{x=2}[/tex] e [tex]\boxed{y=9}[/tex] de dois modos.

Justificativa 1: Podemos reescrever a equação [tex]11\cdot y + x = 101[/tex] como [tex]y\; y+x=101[/tex] e utilizar o esqueminha da adição:

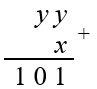
Pelo esquema, podemos notar que a soma dos algarismos das unidades é [tex]1[/tex] ou [tex]11[/tex]. Mas [tex]x[/tex] e [tex]y[/tex] são algarismos não nulos, logo [tex]x+y\ne 1[/tex], donde [tex]x+y=11[/tex] e podemos melhorar nosso esqueminha da adição.

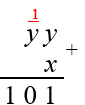
Observando, agora, a coluna das dezenas, concluímos que [tex]1+y=10[/tex] e, portanto, [tex]\boxed{y=9}[/tex]. Como sabemos que [tex]x+y=11[/tex], segue que [tex]\boxed{x=2}[/tex].
Justificativa 2: Da equação [tex]11\cdot y + x = 101[/tex], segue que [tex]11\cdot y=101-x[/tex], ou seja, [tex]101-x[/tex] é um múltiplo de [tex]11[/tex]. Como [tex]x[/tex] é um algarismo não nulo, podemos testar para quais valores de [tex]x[/tex] a diferença [tex]101-x[/tex] é um número múltiplo de [tex]11[/tex]. Vejamos:

[tex]x[/tex]	[tex]101-x[/tex]
[tex]1[/tex]	[tex]100[/tex]
[tex]2[/tex]	[tex]99[/tex]

Como [tex]99[/tex] é um múltiplo de [tex]11[/tex], o próximo múltiplo de [tex]11[/tex] da nossa lista só irá aparecer onze linhas abaixo, ou seja, para [tex]x=2+11=13[/tex]. Mas [tex]13[/tex] não é um algarismo; portanto, [tex]x=2[/tex]. Se você ficou com dúvidas, veja mais algumas linhas da tabela.

[tex]x[/tex]	[tex]101-x[/tex]	Observações
[tex]1[/tex]	[tex]100[/tex]	[tex]100[/tex] não é múltiplo de [tex]11[/tex].
[tex]2[/tex]	[tex]99[/tex]	[tex]99[/tex] é múltiplo de [tex]11[/tex].
[tex]3[/tex]	[tex]98[/tex]	[tex]98[/tex] não é múltiplo de [tex]11[/tex].
[tex]4[/tex]	[tex]97[/tex]	[tex]97[/tex] não é múltiplo de [tex]11[/tex].
[tex]5[/tex]	[tex]96[/tex]	[tex]96[/tex] não é múltiplo de [tex]11[/tex].
[tex]6[/tex]	[tex]95[/tex]	[tex]95[/tex] não é múltiplo de [tex]11[/tex].
[tex]7[/tex]	[tex]94[/tex]	[tex]94[/tex] não é múltiplo de [tex]11[/tex].
[tex]8[/tex]	[tex]93[/tex]	[tex]93[/tex] não é múltiplo de [tex]11[/tex].
[tex]9[/tex]	[tex]92[/tex]	[tex]92[/tex] não é múltiplo de [tex]11[/tex].
[tex]10[/tex]	[tex]91[/tex]	[tex]10[/tex] não é algarismo.
[tex]11[/tex]	[tex]90[/tex]	[tex]11[/tex] não é algarismo.
[tex]12[/tex]	[tex]89[/tex]	[tex]12[/tex] não é algarismo.
[tex]13[/tex]	[tex]88[/tex]	[tex]13[/tex] não é algarismo.

De qualquer forma, [tex] \,\fcolorbox{black}{#eee0e5}{$x=2$}\,\,[/tex], [tex] \,\fcolorbox{black}{#eee0e5}{$y=9$}\,\,[/tex] e [tex] \,\,\fcolorbox{black}{#eee0e5}{$z=1$}\,[/tex].

---

Solução elaborada pelos Moderadores do Blog.