Problema
(Indicado a partir do 9º ano do E. F.)
Qual é a menor área de um quadrado inscrito em um quadrado de lado [tex]a[/tex]?
Solução
Perceba que, ao inscrever um quadrado em um quadrado de lado [tex]a[/tex], criamos quatro triângulos retângulos congruentes (Tente mostrar essa afirmação!).
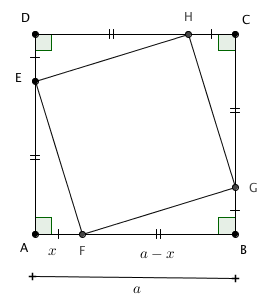
Indicando por [tex]x[/tex] a medida de um dos catetos, ao aplicarmos o teorema de Pitágoras em um dos triângulos retângulos, obtemos que o quadrado da medida do lado do quadrado inscrito (que coincide com sua área) será [tex]x^2 + (a – x)^2 = 2x^2 – 2ax + a^2[/tex].
Note que a área do quadrado inscrito é função de [tex]x[/tex], [tex]A=A(x)[/tex], assim:
- [tex]A(x)=2x^2 – 2ax + a^2[/tex].
Logo, para calcular a área mínima, basta lembrar de como calcular o valor mínimo de uma função quadrática. Então a área mínima será dada por:
- [tex] \, -\dfrac{(-2a)^2 – 4 \cdot 2 \cdot a^2}{4 \cdot 2} = \dfrac{a^2}{2}[/tex].
Portanto, a área mínima de um quadrado inscrito em um quadrado de lados com comprimento [tex]a[/tex] é [tex]\boxed{A=\dfrac{a^2}{2}}[/tex].
Solução elaborada pelos Moderadores do Blog.
Visualização do problema e da solução
Para ajudar na visualização do problema e da solução em alguns casos particulares do quadrado inicial, utilize o applet disponibilizado abaixo.
1) Clique aqui para abrir o applet. (O applet abrirá em outra janela.)
2) Aguarde o aplicativo carregar completamente.
3) Do lado esquerdo da janela que se abriu, o applet mostrará vários inscritos em um quadrado inicial. Para definir esse quadrado inicial, escolha um valor para o comprimento de seu lado, movendo horizontalmente o ponto a. Em seguida, clique no ícone ► que aparece no canto inferior esquerdo do aplicativo, para obter vários quadrados inscritos no quadrado inicial e suas respectivas áreas.
4) Enquanto na janela esquerda o applet mostrará as áreas dos vários quadrados inscritos no quadrado inicial definido, a janela da direita mostrará o gráfico da função que descreve a área desses quadrados inscritos, em função da distância entre os vértices A e F. Nesse gráfico estão destacados dois pontos:
- o vértice V da parábola, cuja coordenada relativa ao eixo vertical (segunda coordenada) nos dá a área mínima procurada;
- o ponto móvel P, cujas coordenadas a cada instante nos dão a área do quadrado inscrito (a segunda coordenada) e a distância entre os vértices A e F (a primeira coordenada).
5) Para parar a construção dos quadrados inscritos, clique no ícone || que aparece no canto inferior esquerdo do aplicativo em movimento. Para reiniciar, clique novamente no no ícone ►.
6) Observamos que o applet ajuda na visualização do resultado; mas, matematicamente, não substitui sua demonstração.
