✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 6º ano do E. F.)
(CP II, 2008 – Adaptado) Uma loja de sanduíches fez a seguinte promoção:
Por apenas R$ 3,00 o sanduíche completo e R$ 2,00 o suco!
Cada cliente poderia fazer seu sanduíche completo com pão francês, colocando um tipo de carne, um tipo de queijo e um molho, além de escolher uma fruta para seu suco. Veja as opções:
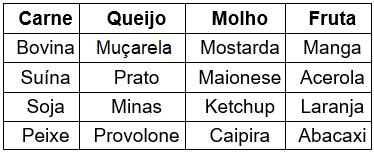
a) Quantos tipos de lanches completos podem ser criados?
b) Quantos tipos de sanduíches completos podem ser criados apenas com a carne bovina?
c) Um cliente acompanhado pela família comprou 7 sanduíches completos e 9 sucos. Pagou a conta e recebeu de troco R$ 1,00. Qual o valor dado pelo cliente para pagamento?
Solução
a) Vamos pensar por etapas.
- Para cada um dos [tex]4[/tex] tipos de carne, existem [tex]4[/tex] tipos de queijo.
Assim, pode-se escolher a carne e o queijo de [tex]4\times 4 = 16[/tex] modos diferentes. - Agora, observe que para cada um desses [tex]16[/tex] modos de escolher a carne e o queijo, existem [tex]4[/tex] modos diferentes de se escolher o molho; totalizando, assim, [tex]16\times 4 = 64[/tex] modos diferentes de formar um sanduíche.
- Por fim, resta escolher o suco e, para isto, perceba que para cada uma dessas [tex]64[/tex] maneiras de se formar um sanduíche, existem [tex]4[/tex] tipos diferentes de sucos. Logo, podem ser criados [tex]64\times 4 = \fcolorbox{black}{#eee0e5}{$256$}[/tex] tipos diferentes de lanches.
b) Como não existem restrições para a escolha do queijo nem do molho, então o total de sanduíches que podem ser formados apenas com a carne bovina é [tex]1\times 4\times 4 = \fcolorbox{black}{#eee0e5}{$16$}[/tex] sanduíches.
c) Como cada sanduíche custa [tex]R$ \;3,00[/tex] e cada suco custa [tex]R$ \;2,00[/tex], o preço a ser pago por [tex]7[/tex] sanduíches e [tex]9[/tex] sucos é
[tex]\qquad 7\times 3,00+9\times 2,00 = R$ \;39,00.[/tex]
Já que o cliente recebeu como troco [tex]R$\, 1,00[/tex], o valor dado por ele para pagamento foi de
[tex]\qquad 39,00+1,00 = \fcolorbox{black}{#eee0e5}{$R\$ \;40,00$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
