Problema
(Indicado a partir do 6º ano do E. F.)
No dia [tex]28[/tex] de junho, o Colégio Militar de Fortaleza promoveu o “Dia do Alívio”, uma atividade que contou com apresentações artísticas dos alunos do colégio, que teve como objetivo proporcionar um momento de integração, descontração e fortalecimento de vínculos fraternos entre os alunos. Essa atividade foi realizada em um palco, em forma de prisma, que pode ser planificado conforme representado a seguir.
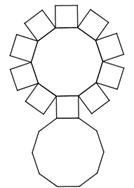
Por curiosidade, um aluno do 6º ano resolveu contar o número de faces [tex](F)[/tex], o número de arestas [tex](A)[/tex] e o número de vértices [tex](V)[/tex] desse prisma, e posteriormente, calculou a expressão [tex](V\times F)\div A[/tex]. Qual o valor obtido?
Adaptado de Colégio Militar de Fortaleza – Sexto Ano EF.
Solução 1
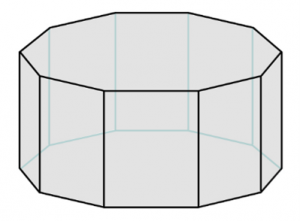
Observe a figura obtida a partir da planificação.
Número de faces [tex]F=12[/tex];
Número de arestas [tex]A=30[/tex];
Número de vértices [tex]V=20[/tex];
Dessa forma, temos: [tex](V\times F)\div A=(20\times 12)\div 30=8.[/tex]
Solução elaborada pelos Moderadores do Blog.

Lembrete para as próximas soluções
Relação de Euler:
Seja [tex]V[/tex] o número de vértices, [tex]F[/tex] o número de faces e [tex]A[/tex] o número de arestas de um poliedro convexo. Então: [tex]V+F=A+2[/tex].
Solução 2
Um prisma pode ser entendido como um poliedro formado pela união dos vértices correspondentes de dois polígonos convexos congruentes (bases) por meio de arestas. Os polígonos devem estar em planos paralelos, mas isso não altera a quantidade de vértices, arestas ou faces.
Por essa interpretação, podemos inferir o seguinte:
1. O número de faces de um prisma é [tex]L+2[/tex], sendo [tex]L[/tex] a quantidade de lados do polígono da base.
2. O número de vértices de um prisma é [tex]2V’[/tex] sendo [tex]V’[/tex] a quantidade de vértices do polígono da base. Como, em um polígono convexo, o número de vértices é igual ao número de lados, podemos expressar a quantidade de vértices do prisma como [tex]2L[/tex].
Pela Relação de Euler para os Poliedros convexos, tem-se que [tex]F + V = A + 2\therefore A = F + V – 2 = 3L[/tex].
Realizando a operação [tex](V\times F)\div A[/tex], temos:
[tex]\qquad(V\times F)\div A = ((L+2)\times2L)\div3L = 2(L+2)\div3[/tex].
No caso do problema, o polígono da base é um decágono. Logo, obtemos:
[tex]\qquad \dfrac{2\cdot (10+2)}{3} = 8.[/tex]
Solução elaborada pelo COM Koreil Guys.
Solução 3
Formando o prisma a partir da planificação, notamos que cada quadrado compartilhará uma aresta com cada decágono.
Portanto, como cada decágono tem [tex]10[/tex] arestas e temos [tex]2[/tex] decágonos, totalizamos, por enquanto, [tex]2 \cdot 10 = 20[/tex] arestas.
Além disso, os quadrados compartilharão uma aresta com cada um dos seus quadrados adjacentes. Inicialmente, nesse caso, tínhamos [tex]2[/tex] arestas de cada [tex]10[/tex] quadrados, porém, como cada quadrado compartilhará uma aresta com cada quadrado adjacente, temos [tex]2 \cdot 10 – 10 = 10.[/tex]
Dado isso, obtemos que o total de arestas é [tex]A = 20 + 10 = 30.[/tex]
Pela relação de Euler, temos que [tex]F+V-A=2[/tex]; dessa forma, temos:
[tex]\qquad 12+V-30=2 \implies
V=32-12=20. [/tex]
Finalmente, obtemos: [tex](20\cdot 12) \div 30=8.[/tex]
Solução elaborada pelo COM Phidias.
Solução 4
Para resolver a questão de forma mais rápida e objetiva, contamos a quantidade de vértices, sendo [tex]10[/tex] na base, por ser um decágono, e [tex]10[/tex] na face superior, sendo assim temos [tex]20[/tex] vértices no total. Para fazer a contagem das faces, contamos uma superior, uma inferior e [tex]10[/tex] nas laterais, totalizando [tex]12[/tex]. Agora, conseguimos descobrir a quantidade de arestas por meio da relação de Euler para poliedros convexos:
[tex]\qquad V-A+F=2 \Rightarrow 20-A+12=2 \Rightarrow A=30.[/tex]
Ou seja, [tex]12[/tex] faces, [tex]30[/tex] arestas e [tex]20[/tex] vértices. Agora, para descobrir o valor que o aluno achou, basta seguir as operações que ele realizou:
[tex]\qquad \dfrac{20 \cdot 12}{30}=\dfrac{2 \cdot 12}{3} = \dfrac{24}{3} = 8.[/tex]
Assim, concluímos que o valor obtido pelo aluno foi [tex]8[/tex].
Solução elaborada pelo COM Potências de Euler.
