Problema
(Indicado a partir do 2º ano do E. M.)
Pedro vai dar um presente a uma amiga e resolveu construir uma caixa, sem tampa, para colocar o presente.
Para construir a caixa, ele utilizou um papel cartão de dimensões [tex]15\ dm[/tex] de comprimento e [tex]10\ dm[/tex] de largura. De cada lado do retângulo, a uma distância [tex]x[/tex] da borda, ele marca as linhas tracejadas conforme mostrado na imagem abaixo.
Finalmente, ele recorta os quatro quadrados de lado [tex]x[/tex] formados pelas linhas tracejadas, dobra a folha sobre as linhas tracejadas para um mesmo lado e cola para formar as laterais da caixa.
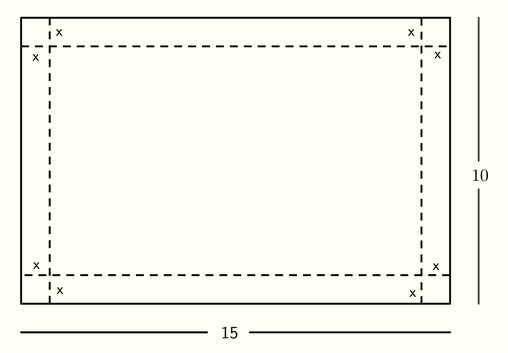
Determine o volume da caixa em função da distância [tex]x[/tex] de dobradura.
Solução
O volume de um paralelepípedo é dado por
[tex]\qquad \qquad V=A_b \times h[/tex], em que [tex]A_b[/tex] é a área da base e [tex]h[/tex] é a altura.
Observando a figura do enunciado, vemos que o retângulo de base do paralelepípedo tem dimensões [tex]\boxed{10-2x} \, [/tex] e [tex] \, \boxed{15-2x}[/tex] e a altura desse paralelepípedo é [tex] \, \boxed{x} \, [/tex].
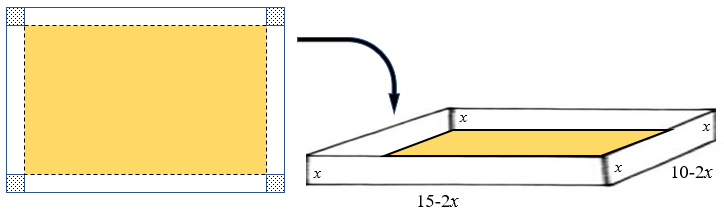
Portanto, o volume da caixa em função de [tex]x[/tex] fica assim definido:
[tex]\qquad V(x)=\underbrace{(10-2x)(15-2x)}_{A_b}\times \underbrace{x}_{altura}=4x^3-50x^2+150x[/tex], com [tex]0\lt x \lt 5[/tex].
Solução elaborada pelos Moderadores do Blog.
