Problema
(Indicado a partir do 9º ano do E. F.)
(Canguru sem Fronteiras – 2016) Uma planta trepadeira foi plantada junto a uma estaca de [tex]1 \, m[/tex] de altura. Durante seu crescimento, a planta se enroscou nessa estaca, girando exatamente [tex]5[/tex] vezes ao redor da mesma, como mostra a figura.
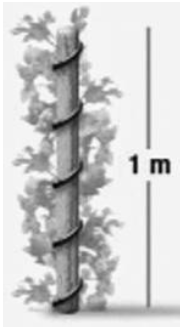
A estaca possui [tex]15 \, cm[/tex] de circunferência e a planta manteve seu crescimento em altura de forma constante.
Qual é o comprimento da planta no momento em que ela alcança o topo da estaca?
Solução
Seja [tex]x[/tex] o comprimento em metros de uma volta da planta na estaca. Observe que, para uma volta apenas, a altura correspondente da estaca é [tex]100:5=20 \, cm[/tex], ou seja, [tex]0,2 \, m \, .[/tex]
Ao desenrolarmos uma volta da planta, obtemos um triângulo retângulo de catetos [tex]0,2 \, m [/tex] e [tex]0,15 \, m \, .[/tex]
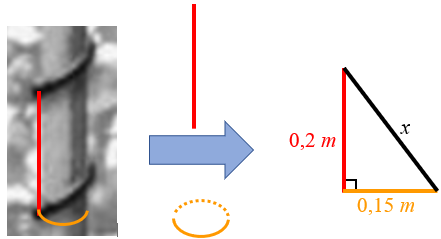
A hipotenusa desse triângulo será a medida correspondente a uma volta da planta na estaca. Assim, pelo Teorema de Pitágoras:
[tex]\qquad x^2=0,2^2+0,15^2[/tex]
[tex]\qquad x=\sqrt{0,0625}[/tex]
[tex]\qquad x=0,25 \, m.[/tex]
Portanto, como a planta dá [tex]5[/tex] voltas na estaca, sua medida total "esticada" é [tex]5 \cdot 0,25=\fcolorbox{black}{#eee0e5}{$1,25 \, m$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
