✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir da 1ª série do E. M.)
(UERJ 2010 – Adaptado) A ilustração a seguir mostra um pistão e seu esquema no plano.
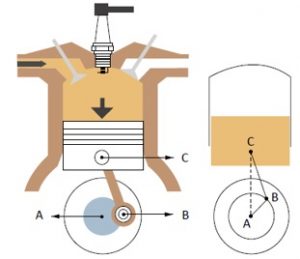
O pistão é ligado, por meio da haste [tex]BC[/tex], a um disco que gira em torno do centro [tex]A[/tex]. No esquema plano, sabemos que o raio [tex]AB[/tex] tem medida de [tex]10\,cm[/tex], o segmento [tex]BC[/tex] tem medida de [tex]40\, cm[/tex] e a medida do ângulo formado entre [tex]AB[/tex] e [tex]BC[/tex] é de [tex]120^\circ[/tex].
Qual a medida do segmento [tex]AC[/tex]?
Um applet para ajudar na visualização do problema
Você pode utilizar este applet para ver o movimento do pistão e, principalmente, observar que a distância entre os pontos [tex]A[/tex] e [tex]C[/tex] varia de acordo com esse movimento.
Instruções:
(1) Espere o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para movimentar manualmente o êmbolo que aparece na tela do applet, clique com o botão esquerdo do mouse sobre o ponto B, mantenha o botão apertado e, em seguida, movimente o mouse para fazer o ponto rodar ao longo da circunferência sobre a qual ele se encontra. (Se você estiver utilizando um celular ou um tablet, toque levemente no ponto B e movimente-o.)
(3) Para fazer uma animação do movimento do pistão, clique com o botão direito do mouse sobre o ponto B e selecione a opção Animação na janelinha que se abriu.
(4) Clique no ícone || que apareceu no canto inferior esquerdo da janela, para parar a animação.
(5) Clique no ícone ► que apareceu no canto inferior esquerdo da janela, para reiniciar a animação.
(6) Se quiser voltar para a visualização inicial, clique nas setinhas circulares que aparecem no canto superior direito da janela.
OBMEP_ srdg, criado com o GeoGebra

Lembrete
Lei dos Cossenos: Em um triângulo [tex]ABC[/tex] qualquer, para lados opostos aos ângulos internos [tex]{\displaystyle {\widehat {A}},{\widehat {B}}}[/tex] e [tex]{\displaystyle {\widehat {C}},} [/tex] com medidas respectivamente [tex]{\displaystyle a,b}[/tex] e [tex]{\displaystyle c,}[/tex] valem as relações:
[tex]\quad { a^{2}=b^{2}+c^{2}-2\cdot b\cdot c\cdot cos{\widehat {A}}\,\!}[/tex];
[tex]\quad {\displaystyle b^{2}=a^{2}+c^{2}-2\cdot a\cdot c\cdot cos{\widehat {B}}\,\!}[/tex];
[tex]\quad {\displaystyle c^{2}=a^{2}+b^{2}-2\cdot a\cdot b\cdot cos{\widehat {C}}\,\!}[/tex].
Solução
No esquema plano do pistão, vamos chamar de [tex]x[/tex] a medida em centímetros do segmento [tex]AC[/tex] e destacar o triângulo [tex]ABC[/tex] abaixo, construído a partir dos dados do problema.
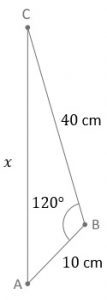
Pela Lei dos Cossenos, temos:
[tex]\qquad x^2=40^2+10^2-2\cdot 40 \cdot 10 \cdot cos\,120^\circ\\
\qquad x^2=1600+100-2\cdot 40 \cdot 10 \cdot \left(-\dfrac{1}{2}\right)\\
\qquad x^2=1600+100+400\\
\qquad x^2=2100.[/tex]
Como [tex]x[/tex] é uma medida de comprimento, [tex]x \geq 0[/tex]; assim:
[tex]\qquad \boxed{x=10\sqrt{21}\approx45,8\, cm}.[/tex]
Solução elaborada pelos Moderadores do Blog.
Você pode utilizar o applet para conferir a solução deste problema.
É só clicar no botão abaixo.
