Problema
(Indicado a partir do 9º ano do E. F.)
Uma arquiteta planejou uma piscina para a casa do seu cliente com o formato de dois setores circulares idênticos, com ângulo central igual a [tex]90^\circ[/tex].
A região disponível no lote do cliente para a construção da piscina é um retângulo de dimensões [tex]4m\times 8m[/tex] e a vista superior da piscina está representada na figura abaixo.
A arquiteta ainda pretende gramar a região que pertence ao retângulo, mas que não faz parte da piscina.
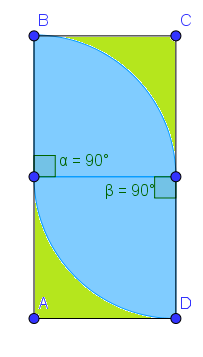
Desta forma, determine:
a) A área da piscina;
b) A área que será gramada.
Solução
a) Como cada setor circular que representa metade da piscina possui ângulo central de [tex]90^\circ[/tex], então a área de cada setor é igual a [tex]\frac{1}{4}[/tex] da área delimitada pela circunferência que define esse setor. Além disso, como a piscina é formada por dois setores idênticos, sua área total será a metade da área de um círculo com o mesmo raio dos setores. Observem que temos [tex]r=4 \, m[/tex], logo a área [tex]A_p[/tex] da piscina poder ser assim calculada:
[tex]\qquad \qquad A_p=\frac{1}{2}\pi 4^2=8\pi \, m^2.[/tex]
Poderíamos ter efetuado os cálculos diretamente:
- Observe que a área de cada um dos dois setores circulares que definem a piscina é dada por [tex]\dfrac{\pi 4^2}{4} =4\pi [/tex].
Portanto, a área total da piscina é de [tex]2 \times(4\pi)= \boxed{8\pi \, m^2}[/tex].
b) Para determinar a área [tex]A_g[/tex] que será gramada, basta observar que [tex]A_g[/tex] é dada pela diferença entre as áreas do terreno retangular e da piscina. Daí:
[tex]\qquad \qquad A_g=4\times8-8\pi[/tex]
[tex]\qquad \qquad A_g=32-8\pi[/tex]
[tex]\qquad \qquad A_g=8(4-\pi) \, m^2.[/tex]
Solução elaborada pelos Moderadores do Blog.
