Problema
(Indicado a partir do 9º ano do E. F.)
Num triângulo equilátero [tex]ABC[/tex], os pontos [tex]M[/tex], [tex]N[/tex] e [tex]P[/tex] são tomados em [tex]\overline{BC}[/tex], [tex]\overline{AC}[/tex] e [tex]\overline{AB}[/tex], respectivamente, de modo que [tex]\overline{AM} \perp \overline{BC}[/tex], [tex]\overline{MN} \perp \overline{AC}[/tex] e [tex]\overline{NP} \perp \overline{AB}[/tex].
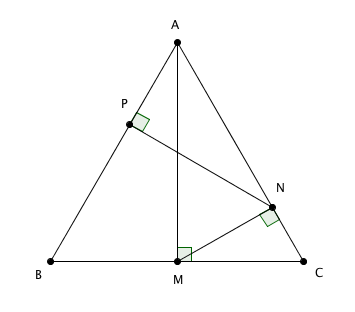
Mostre que a interseção de [tex]\overline{NP}[/tex] e [tex]\overline{AM}[/tex] é ponto médio de [tex]\overline{AM}[/tex].

Lembretes
Alguns resultados sobre ângulos internos de um triângulo:
[tex] \color{#800000}{(*)}[/tex] A soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex].
[tex] \color{#800000}{(**)}[/tex] Todo triângulo equilátero tem ângulos internos de [tex]60^{\circ}[/tex].
[tex] \color{#800000}{(***)}[/tex] Ângulos opostos pelo vértice (OPV) têm a mesma medida.
Solução 1
Note que, a partir das proposições [tex] \color{#800000}{(*)}[/tex], [tex] \color{#800000}{(**)}[/tex] e [tex] \color{#800000}{(***)}[/tex] do Lembrete, podemos completar as medidas de alguns ângulos da figura inicial, de acordo com a figura a seguir.
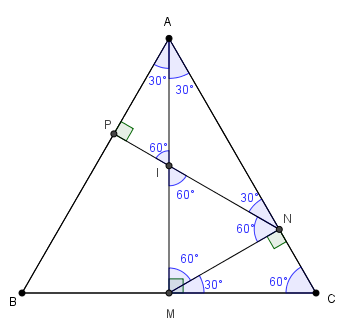
Agora, observe que:
- o triângulo [tex]IMN[/tex] é equilátero, logo [tex]IM=MN=NI[/tex],
- o triângulo [tex]AIN[/tex] é isósceles, logo [tex]NI=IA[/tex].
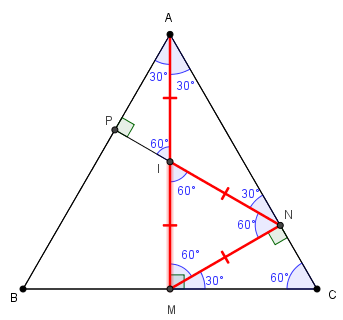
Dessa forma, [tex]IM=IA[/tex] e, com isso, temos que [tex]I[/tex] é ponto médio de [tex]\overline{AM}[/tex].
Solução elaborada pelos Moderadores do Blog.
Solução 2
Para aqueles que gostam de ver para crer, vamos apresentar uma segunda solução, na qual mostraremos explicitamente que o comprimento de [tex]\overline{AI}[/tex] é a metade do comprimento de [tex]\overline{AM}[/tex], sendo [tex]I[/tex] o ponto de interseção de [tex]\overline{NP}[/tex] e [tex]\overline{AM}[/tex].
Inicialmente, observe que, a partir duas proposições [tex] \color{#800000}{(*)}[/tex] e [tex] \color{#800000}{(**)}[/tex] do Lembrete, podemos completar as medidas de alguns ângulos da figura inicial, como mostramos a seguir.
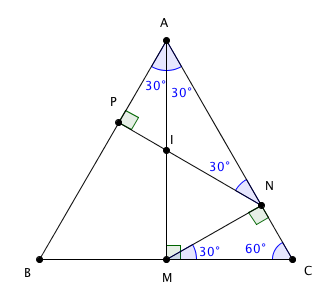
Seja [tex]a[/tex] a medida do lado do triângulo equilátero [tex]ABC[/tex].
- No triângulo [tex]AMC[/tex], temos:
[tex]\qquad \cos 30^{\circ} = \dfrac{AM}{a}\\ [/tex]
Mas, em um triângulo equilátero uma altura é também mediana; assim, [tex]M[/tex] é ponto médio de [tex]\overline{AM}[/tex]. Logo, segue da igualdade anterior que:
[tex]\qquad \dfrac{\sqrt{3}}{2} = \dfrac{AM}{a} [/tex][tex]\qquad \fcolorbox{black}{#eee0e5}{$AM = \dfrac{a\sqrt{3}}{2}$} \, .\qquad \color{#800000}{(i)}[/tex]
- No triângulo [tex]MNC[/tex], temos
[tex]\qquad\text{sen}\, 30^{\circ} = \dfrac{NC}{MC} \\
[/tex]
[tex]\qquad\text{sen}\, 30^{\circ} = \dfrac{NC}{\frac{a}{2}}\\
[/tex]
[tex]\qquad \dfrac{1}{2} = \dfrac{NC}{\frac{a}{2}} [/tex]
[tex]\qquad \boxed{NC = \dfrac{a}{4}}.\qquad \color{#800000}{(ii)}[/tex]
- [tex]AN + NC = AC [/tex]
[tex]AN \stackrel{\textcolor{#800000}{(ii)}}{=} a-\dfrac{a}{4}[/tex].
[tex]\boxed{AN = \dfrac{3a}{4}}. \qquad \color{#800000}{(iii)}[/tex]
- No triângulo [tex]NPA[/tex], temos:
[tex]\qquad \text{sen}\, 30^{\circ} =\dfrac{AP}{AN}\\
[/tex]
[tex]\qquad \text{sen}\, 30^{\circ} \stackrel{\textcolor{#800000}{(iii)}}{=} \dfrac{AP}{\dfrac{3a}{4}}[/tex]
[tex]\qquad \dfrac{1}{2} = \dfrac{AP}{\frac{3a}{4}}[/tex]
[tex]\qquad \boxed{AP = \dfrac{3a}{8}}.\qquad \color{#800000}{(iv)}[/tex]
- No triângulo [tex]API[/tex], temos:
[tex]\qquad \cos 30^{\circ} = \dfrac{AP}{AI} \\
[/tex]
[tex]\qquad \cos 30^{\circ} \stackrel{\textcolor{#800000}{(iv)}}{=} \dfrac{\frac{3a}{8}}{AI} [/tex]
[tex]\qquad \dfrac{\sqrt{3}}{2} = \dfrac{\frac{3a}{8}}{AI} [/tex]
[tex]\qquad \fcolorbox{black}{#eee0e5}{$AI = \dfrac{a\sqrt{3}}{4}$} \, .\qquad \color{#800000}{(v)}[/tex]De [tex] \color{#800000}{(i)}[/tex] e [tex] \color{#800000}{(v)}[/tex], segue que [tex]I[/tex] é ponto médio de [tex]\overline{AM}[/tex].
Solução elaborada pelos Moderadores do Blog.
