Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)
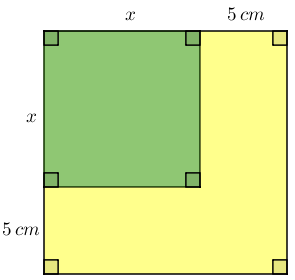
Na figura abaixo, qual deve ser o valor de [tex]x[/tex] para que a área pintada de amarelo seja [tex]105 \, cm^2[/tex]?
Solução
Vamos considerar que o valor de [tex]x[/tex] está expresso em centímetros.
Observe que a área pintada de amarelo é a diferença entre a área do quadrado externo, com lados medindo [tex](x+5)[/tex] centímetros, e a área do quadrado interno pintado de verde, cujos lados medem [tex]x[/tex] centímetros.
Assim, segue que:
[tex]\qquad A_{amarelo}=\left(x+5\right)^2-x^2[/tex]
[tex]\qquad 105=\left(x+5\right)^2-x^2[/tex]
[tex]\qquad 105=\cancel{x^2}+10x+25-\cancel{x^2}[/tex]
[tex]\qquad 10x=105-25[/tex]
[tex]\qquad 10x=80[/tex]
[tex]\qquad x=8.[/tex]
Portanto, [tex] \, \fcolorbox{black}{#eee0e5}{$x=8 \, cm$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo desta página em PDF. Mas, para abrir esse arquivo, é necessário que você tenha o Adobe Acrobat Reader instalado no dispositivo que você está utilizando. Caso não tenha, é só clicar AQUI para fazer o download. |
