✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
(XXVIII OPM, 2009 – Adaptado) Dona Nilza serve uma deliciosa “média” aos funcionários da empresa onde trabalha.
Cada 220 ml desse “café com leite” tem 60% de leite e 40% de café e é servido em “simpáticas” xícaras de 240 ml.

A funcionária Maria Clara pediu uma “média”. Mas, depois de ser servida, Maria Clara pediu para Dona Nilza acrescentar um pouco mais de leite à sua “média”, de modo que a nova mistura passe a ter 80% de leite.
Que quantidade de leite deve ser acrescentada à “média” da Maria Clara?
Dona Nilza conseguirá atender a esse pedido?
Solução
Observe que, por padrão, dos [tex]220 \, ml[/tex] de cada média servida por D. Nilza, [tex]40 \%[/tex] corresponde ao café. Vamos calcular a quantidade em [tex]ml[/tex] correspondente a esse percentual, uma vez que, na nova mistura, essa quantidade não se modificará, pois à mistura será acrescentado apenas leite. Uma regrinha de três resolve isso.
\begin{array}{c c c}
\qquad 220 \, ml & \text{————–} & 100\% \qquad \\
\qquad c \, ml & \text{————–} & 40\% \qquad \end{array}
Se [tex]c[/tex] for a quantidade em [tex]ml[/tex] servida na média, então [tex]c \times 100=220 \times 40.[/tex]
Assim, segue que [tex]c =\dfrac{220 \times 40}{100}=88 \, ml[/tex].
Dessa forma, os [tex]220 \, ml[/tex] da média da D. Nilza têm [tex]88 \, ml[/tex] de café e [tex]220-88=132 \, ml[/tex] de leite.
Para resolver o problema, vamos analisar o que representa o acréscimo de [tex]20\%[/tex] de leite solicitado pela Maria Clara. Suponha que [tex]L[/tex] seja a quantidade em mililitros correspondente a esse acréscimo e observe no esqueminha abaixo as duas composições: [tex]\boxed{60\%+40\%}[/tex] e [tex]\boxed{80\%+20\%} \, .[/tex]
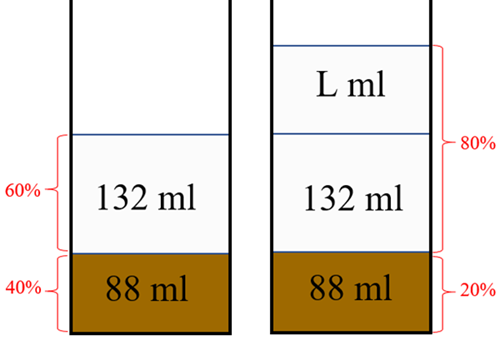
Com uma nova regrinha de três, vamos determinar o valor de [tex]L.[/tex] Observe.
\begin{array}{c c c}
\qquad 88 \, ml & \text{————–} & 20\% \qquad \\
\qquad (132+L) \, ml & \text{————–} & 80\% \qquad \end{array}
Veja que [tex]88 \times 80=20 \times \left(132+L \right);[/tex] assim, segue que
[tex]\qquad 132+L=\dfrac{88 \times 80}{20}[/tex]
[tex]\qquad 132+L=88 \times 4[/tex]
[tex]\qquad 132+L=352[/tex]
[tex]\qquad L=220 \, ml.[/tex]
Bem, a quantidade de leite correspondente ao acréscimo solicitado por Maria Clara é [tex] \, \fcolorbox{black}{#eee0e5}{$L=220 \, ml$} \, [/tex]; agora, se Dona Nilza conseguirá atender a esse pedido é uma outra conversa…
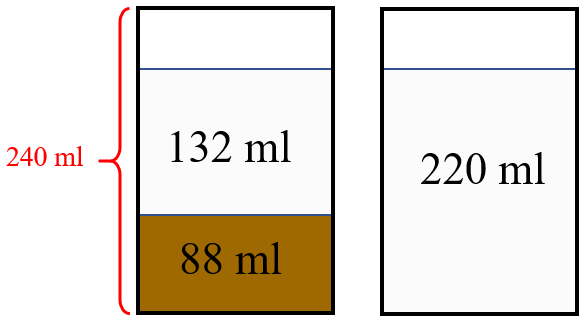
- Repare que [tex]220 \, ml[/tex] é exatamente a quantidade correspondente a uma média comum que a D. Nilza serve! Isso mesmo; acrescentar [tex]20\%[/tex] a mais de leite à média normalmente servida significa dobrar a quantidade de líquido da mistura original.
Como os recipientes utilizados para servir as médias comportam [tex]240 \, ml[/tex], D. Nilza não conseguirá “acrescentar à média” a quantidade extra de leite solicitada. Caso ela resolva atender ao pedido de Maria Clara, terá que servir dois recipientes: um com a média normal e um com a porção extra de leite.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
