✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
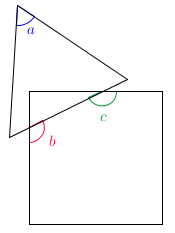
Na figura aparecem um quadrado, um triângulo equilátero e três ângulos identificados por suas medidas em graus [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex].
Determinar [tex]a+b+c[/tex].

Lembretes
✐ Para que você acompanhe a solução deste problema, ajuda lembrar que:
- Os ângulos internos de um triângulo equilátero são congruentes e medem [tex]60^{\circ}[/tex] cada.
- A soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex]. (Se precisar, visite esta página.)
Solução
- Observe inicialmente que, como o triângulo da figura inicial é equilátero, [tex]\boxed{a=60^{\circ}} \, .\quad \textcolor{#800000}{(i)}[/tex]
- Por outro lado, o triângulo [tex]ABC[/tex] mostrado na figura abaixo é um triângulo retângulo cujos ângulos agudos medem [tex]180^{\circ}-b[/tex] e [tex]180^{\circ}-c[/tex].
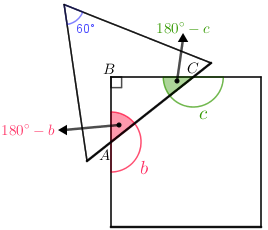
Sabemos que a soma dos ângulos internos do triângulo [tex]ABC[/tex] é [tex]180^{\circ}[/tex], portanto:
[tex]\qquad \left(180^{\circ}-b\right)+\left(180^{\circ}-c\right)+90^{\circ}=180^{\circ}[/tex]
[tex]\qquad b+c=180^{\circ}+180^{\circ}+90^{\circ}-180^{\circ}[/tex]
[tex]\qquad \boxed{b+c=270^{\circ}}. \, \quad \textcolor{#800000}{(ii)}[/tex]
Finalmente, por [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(ii)}[/tex], segue que:
[tex]\qquad a+b+c=a+(b+c)=60^{\circ}+270^{\circ} \, [/tex],
isto é, [tex]\fcolorbox{black}{#eee0e5}{$a+b+c=330^{\circ}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
