✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)
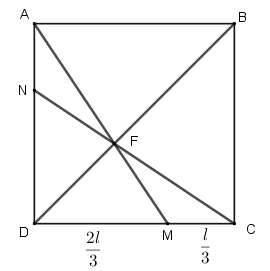
Temos um quadrado [tex]ABCD[/tex].
- Tomemos um ponto [tex]M[/tex] no lado [tex]\overline{CD}[/tex] tal que [tex]DM=2 \cdot MC[/tex].
- Seja [tex]F[/tex] o ponto de interseção de [tex]\overline{BD}[/tex] e [tex]\overline{MA}[/tex].
- A reta determinada por [tex]F[/tex] e [tex]C[/tex] intersecta [tex]\overline{AD}[/tex] em [tex]N[/tex].
Nessas condições, determine [tex]\dfrac{ND}{AN}[/tex].
Notação: Denotamos o segmento definido por dois pontos, digamos [tex]X \, [/tex] e [tex] \, Y[/tex], por [tex]\overline {XY}[/tex] e o seu comprimento por [tex]XY[/tex].

Lembretes
(1) Caso de congruência L.A.L. (lado – ângulo – lado): Se dois triângulos têm ordenadamente congruentes dois lados e o ângulo por eles definido, então estes triângulos são congruentes.
(2) Os ângulos da base de um triângulo isósceles são congruentes.
(3) Caso de congruência A.L.A. (ângulo – lado – ângulo): Se dois triângulos têm ordenadamente congruentes dois ângulos e o lado compreendido por eles, então estes triângulos são congruentes.
(Se você não se lembra desses resultados, clique AQUI.)
Solução
Observe a figura a seguir, construída a partir dos dados do problema. Estamos supondo que o comprimento dos lados do quadrado [tex]ABCD[/tex] seja [tex]l.[/tex]
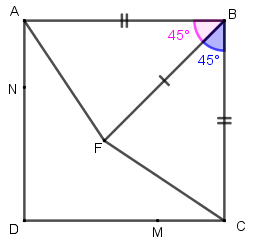
- Como [tex]F[/tex] é ponto da diagonal [tex]\overline{BD}[/tex] e a diagonal de um quadrado é também uma bissetriz, então os ângulos [tex]F\hat B A[/tex] e [tex]F\hat B C[/tex] são congruentes.
- Os segmentos [tex]\overline{AB} \, [/tex] e [tex] \, \overline{BC}[/tex] são lados de um quadrado; logo, são congruentes.
- O segmento [tex]\overline{BF}[/tex] é comum aos triângulos [tex]ABF[/tex] e [tex]CBF.[/tex]
Assim, pelo caso L.A.L., os triângulos [tex]ABF[/tex] e [tex]CBF[/tex] são congruentes. Dessa congruência concluímos que os segmentos [tex]\overline{FA} \, [/tex] e [tex] \, \overline{FC}[/tex] são congruentes, assim como os ângulos [tex]B\hat A F[/tex] e [tex]B\hat C F.[/tex]
Observemos agora os triângulos [tex]AFN[/tex] e [tex]CFM[/tex].
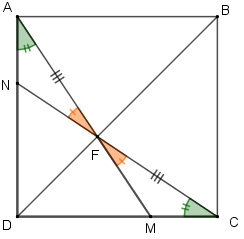
- Os ângulos [tex]N\hat A F[/tex] e [tex]M\hat C F[/tex] são complementares, respectivamente, dos ângulos [tex]B\hat A F[/tex] e [tex]B\hat C F[/tex] e estes são congruentes. Assim, [tex]N\hat A F[/tex] e [tex]M\hat C F[/tex] são também ângulos congruentes.
- Os segmentos [tex]\overline{FA} \, [/tex] e [tex] \, \overline{FC}[/tex] são congruentes.
- Os ângulos [tex]A\hat F N[/tex] e [tex]C\hat F M[/tex] são opostos pelo vértice; logo, são congruentes.
Assim, pelo caso A.L.A., os triângulos [tex]AFN[/tex] e [tex]CFM[/tex] são congruentes. Dessa congruência concluímos particularmente que os segmentos [tex]\overline{AN} \, [/tex] e [tex] \, \overline{CM}[/tex] são congruentes.
Por fim, temos que:
- Como [tex]\overline{AN} \, [/tex] e [tex] \, \overline{CM}[/tex] são congruentes, então [tex]AN=MC;\qquad \textcolor{#800000}{(i)}[/tex]
- Como [tex]ABCD[/tex] é quadrado, [tex]AD=DC;\qquad \textcolor{#800000}{(ii)}[/tex]
- [tex]M[/tex] é ponto do lado [tex]\overline{CD}[/tex]; logo, [tex]DC=DM+MC;\qquad \textcolor{#800000}{(iii)}[/tex]
- [tex]N[/tex] é ponto do lado [tex]\overline{AD}[/tex]; logo, [tex]AD=AN+ND.\qquad \textcolor{#800000}{(iv)}[/tex]
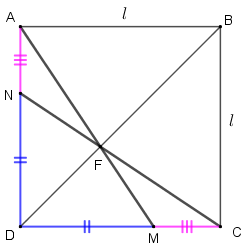
Assim, segue que:
[tex]\qquad AD\stackrel{\textcolor{#800000}{(ii)}}{=}DC\\
\qquad AN+ND \stackrel{\textcolor{#800000}{(iii) \, , \, (iv)}}{=}DM+MC\\
\qquad MC+ND \stackrel{\textcolor{#800000}{(i)}}{=}DM+MC\\
\qquad \cancel{MC}+ND =DM+\cancel{MC}\\
\qquad \boxed{ND =DM}.\\[/tex]
Com isso:
[tex]\qquad \dfrac{ND}{AN}=\dfrac{DM}{AN}\stackrel{\textcolor{#800000}{(i)}}{=}\dfrac{DM}{MC}.[/tex]
Mas o problema nos garante que [tex]DM=2 \cdot MC[/tex], logo:
[tex]\qquad \dfrac{ND}{AN}=\dfrac{DM}{MC}=\dfrac{2 \cdot \cancel{MC}}{\cancel{MC}}=2.[/tex]
Portanto, [tex] \, \fcolorbox{black}{#eee0e5}{$\dfrac{ND}{AN}=2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
