✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 8º ano do E. F.- Nível de dificuldade: Fácil)
(Adaptado da XXIX OPM, 2010) Os times de vôlei masculino e feminino e mais o time de basquete feminino da escola Reino Feliz se classificaram para a final dos jogos regionais.
Para incentivar os times, os alunos da escola decidiram criar uma bandeira que será levada nas três finais das quais os times irão participar.
Essa bandeira tem a forma retangular e foi dividida em três regiões com áreas iguais, a partir de um segmento paralelo aos lados do retângulo e com comprimento [tex]x[/tex], para que cada região representasse um time.
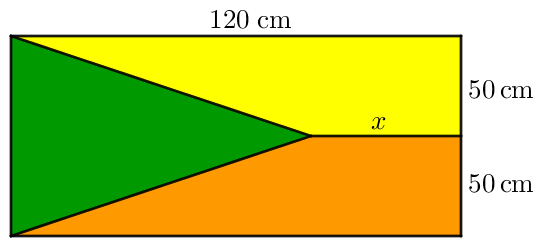
Determinar o comprimento x, em metros.
Solução 1
Observe, inicialmente, que a área [tex]B[/tex] da bandeira é dada por:
[tex]\qquad B=(50+50) \times 120[/tex]
[tex]\qquad B=100 \times 120[/tex]
[tex]\qquad B= 12000\,\text{cm}^2.[/tex]
Como a bandeira foi dividida em três regiões com áreas iguais, a área [tex]Re[/tex] de cada região é dada por:
[tex]\qquad Re=\dfrac{12000}{3}[/tex]
[tex]\qquad Re= 4000\,\text{cm}^2.[/tex]
Prolongando o segmento de comprimento [tex]x[/tex] de modo a obtermos uma altura para o triângulo colorido de verde na bandeira, obtemos que:
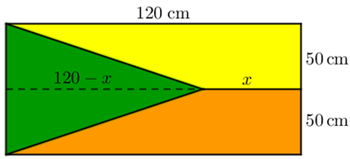 [tex]\qquad \textcolor{#009900}{A_{verde}}=\dfrac{\text{base} \times \text{altura}}{2}\\
[tex]\qquad \textcolor{#009900}{A_{verde}}=\dfrac{\text{base} \times \text{altura}}{2}\\\qquad \textcolor{#009900}{A_{verde}}=\dfrac{100 \times \left(120-x\right)}{2}\\
\qquad \textcolor{#009900}{4000}=\dfrac{100 \times \left(\text{120$-x$}\right)}{2}\\
\qquad 8000=12000-100x\\
\qquad 80=120-x\\
\qquad x=40\,\text{cm}.[/tex]
O esquema de conversão abaixo permite concluir que o comprimento [tex]x[/tex] é [tex]\;\fcolorbox{black}{#eee0e5}{$0,4 \text{ metros}\,$}\,.[/tex]
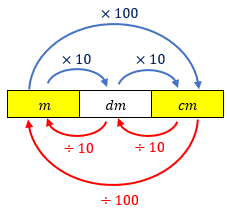
Solução elaborada pelos Moderadores do Blog.
Solução 2
(Indicada a partir do 9º ano do E. F.)
Observe, inicialmente, que a área [tex]B[/tex] da bandeira é dada por:
[tex]\qquad B=(50+50) \times 120[/tex]
[tex]\qquad B=100 \times 120[/tex]
[tex]\qquad B= 12000\,\text{cm}^2.[/tex]
Como a bandeira foi dividida em três regiões com áreas iguais, a área [tex]Re[/tex] de cada região é dada por:
[tex]\qquad Re=\dfrac{12000}{3}[/tex]
[tex]\qquad Re= 4000\,\text{cm}^2.[/tex]
Calculando a área de qualquer um dos trapézios que aparecem na figura, por exemplo o alaranjado, vemos que:
[tex]\qquad \textcolor{#F88017}{A_{laranja}}=\dfrac{\left(\text{base maior + base menor}\right) \times \text{altura}}{2}\\
\qquad \textcolor{#F88017}{A_{laranja}}=\dfrac{\left(120 + x\right) \times 50}{2}\\
\qquad \textcolor{#F88017}{4000}=\dfrac{\left(120 + x\right) \times 50}{2}\\
\qquad 160=120 + x\\
\qquad x=40\,\text{cm}.[/tex]
O esquema de conversão abaixo permite concluir que o comprimento [tex]x[/tex] é [tex]\;\fcolorbox{black}{#eee0e5}{$0,4 \text{ metros}\,$}\,.[/tex]

Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
