✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F.- Nível de dificuldade: Médio)
Em um triângulo [tex]ABC[/tex], o comprimento do lado [tex]AB[/tex] é [tex]2\text{ cm}[/tex], o comprimento do lado [tex]BC[/tex] é [tex]4\text{ cm}[/tex] e o ângulo interno cujo vértice é [tex]B[/tex] mede [tex]72^\circ.[/tex]
Feita uma rotação, no sentido horário, do triângulo [tex]ABC[/tex] em torno do vértice [tex]B[/tex], foi obtido o triângulo [tex]A’BC’.[/tex]
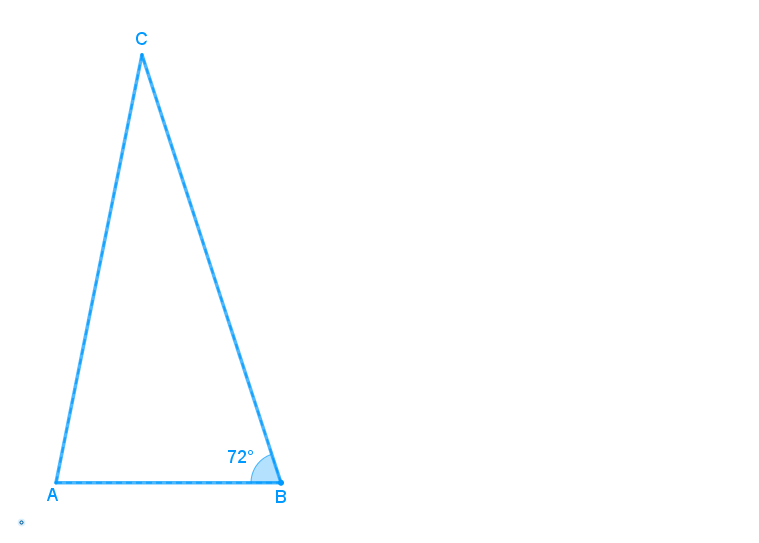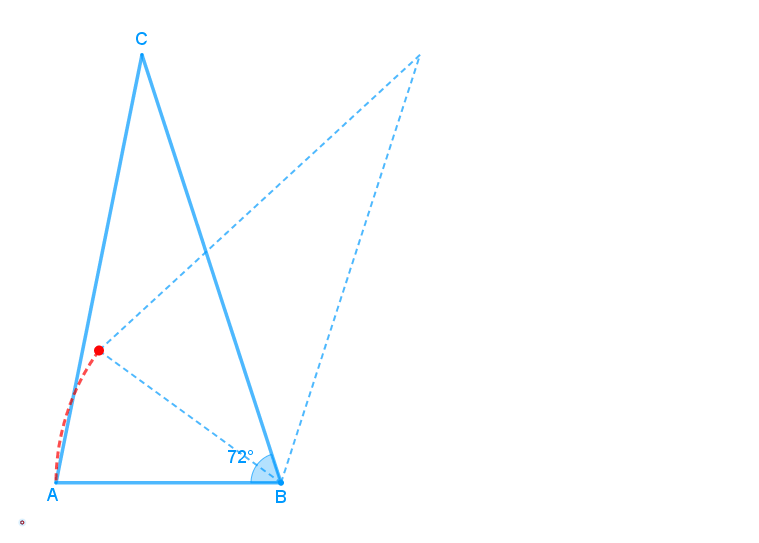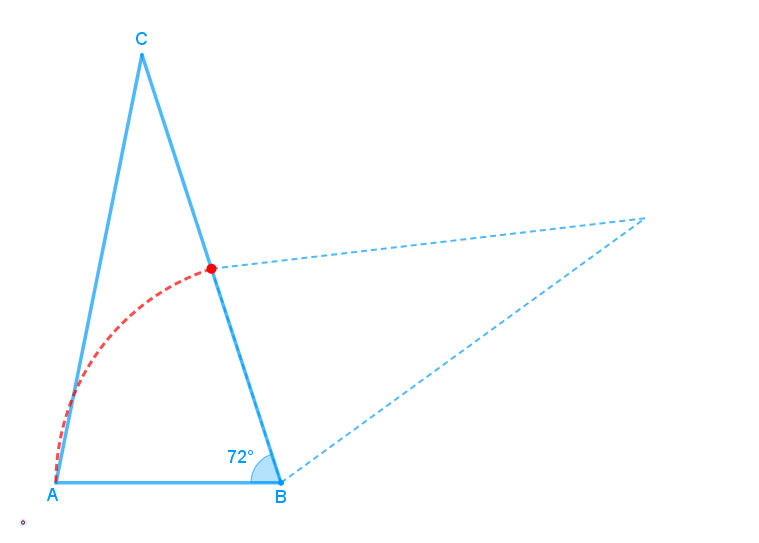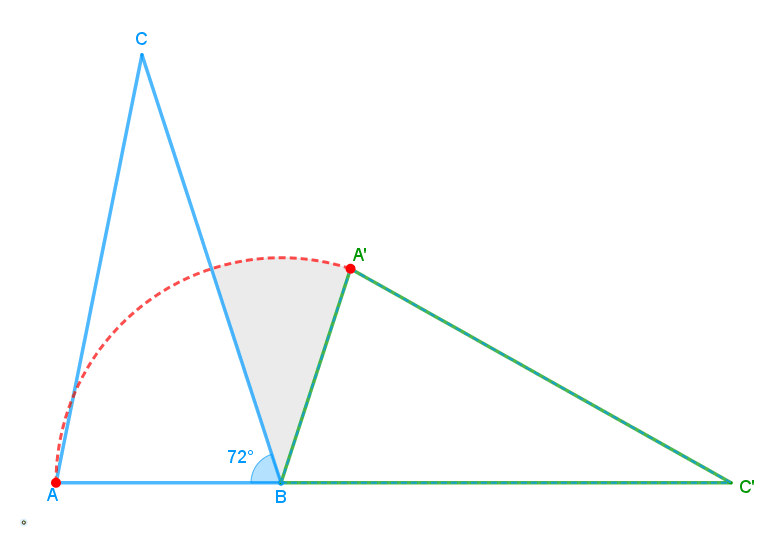
Sabendo-se que os pontos [tex]A[/tex], [tex]B[/tex] e [tex]C'[/tex] são colineares e que o arco [tex]\stackrel{\frown}{AA’}[/tex] foi o descrito por [tex]A[/tex] durante a rotação, determine a medida da área sombreada.
Um applet para ajudar
Instruções:
(1) Espere o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para iniciar a rotação do triângulo [tex]ABC[/tex], clique na setinha que aparece no canto inferior esquerdo do aplicativo.
(3) Depois que a rotação for finalizada, para fazer uma nova rotação, clique nas setinhas circulares que aparecem no canto superior direito do aplicativo e, em seguida, clique novamente na setinha que aparece no canto inferior esquerdo do aplicativo.
(4) Você pode parar uma rotação em curso clicando no ícone || que aparece no canto inferior esquerdo enquanto a animação está ocorrendo. Para reiniciar o movimento, basta clicar na setinha que substituiu o ícone || no canto inferior esquerdo.
OBMEP_ srdg, criado com o GeoGebra
Solução
O triângulo [tex]A’BC'[/tex] é o resultado da rotação do triângulo [tex]ABC[/tex] em torno do ponto [tex]B[/tex] de modo que os pontos [tex]A[/tex], [tex]B[/tex] e [tex]C'[/tex] ficassem colineares. Assim, os triângulos [tex]ABC[/tex] e [tex]A’BC'[/tex] são congruentes, ou seja, as medidas dos lados e dos ângulos de um são iguais às medidas dos respectivos lados e ângulos do outro.
Em particular, a medida do ângulo [tex]A’\hat{B}C'[/tex] é [tex]72^\circ.[/tex]
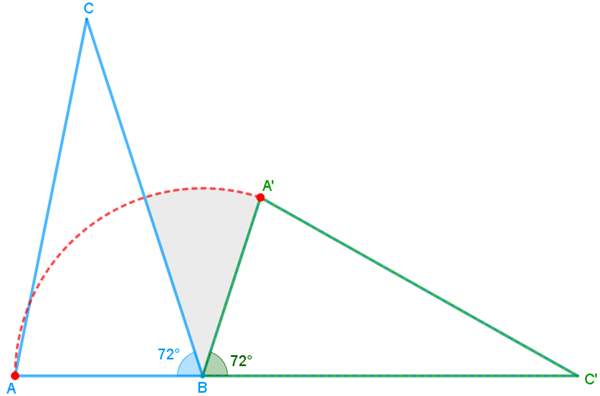
Dessa forma, como os pontos [tex]A[/tex], [tex]B[/tex] e [tex]C'[/tex] são colineares, temos que a medida do ângulo [tex]A\hat{B}C'[/tex] é [tex]180^\circ[/tex] e, portanto, a medida do ângulo [tex]C\hat{B}A'[/tex] é [tex]180^\circ-72^\circ-72^\circ=\boxed{\,36^\circ\,}.[/tex]
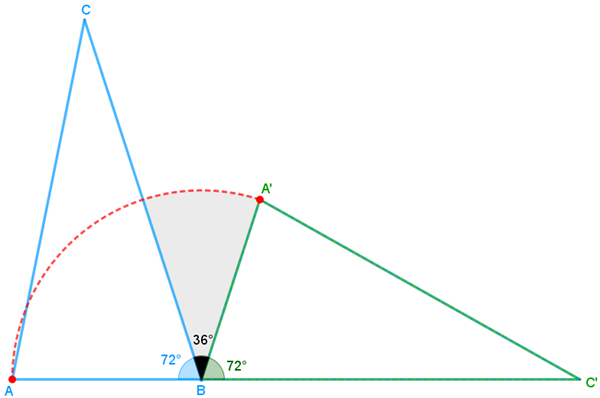
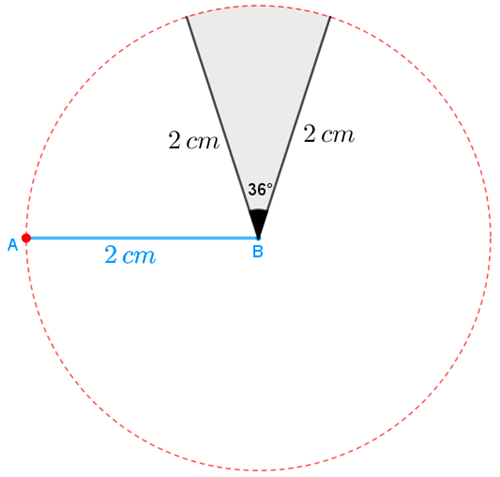
Assim, a área sombreada é um setor circular correspondente a um ângulo de [tex]36^\circ[/tex] em uma circunferência de raio [tex]2\text{ cm}.[/tex]
Sabemos que a medida da área de um setor circular de raio [tex]R[/tex] e [tex]\alpha[/tex] graus é dada pela expressão [tex] \boxed{\dfrac{\pi\cdot R^{\, 2} \cdot \alpha}{360}}[/tex]; logo, a medida [tex]S[/tex] da área sombreada é:
[tex] \qquad \qquad S=\dfrac{\pi\cdot 2^{\, 2} \cdot 36}{360}\\
\qquad \qquad S=\dfrac{\pi\cdot 4}{10}\\
\qquad \qquad \fcolorbox{black}{#eee0e5}{$\,S=\dfrac{2\,\pi}{5}\,\text{cm}^2$}\\
\qquad \qquad \fcolorbox{black}{#eee0e5}{$\,S \approx 1,26\text{ cm}^2$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
