✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
Na figura abaixo, vemos o gráfico da função quadrática assim definida: [tex]f(x)=x^2+bx+c.[/tex]
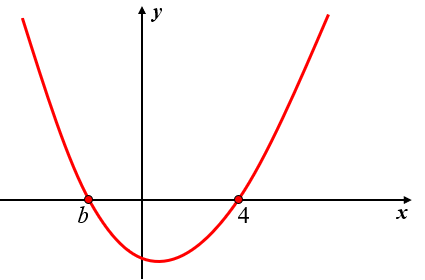
Determine [tex]f(8).[/tex]

Lembretes para Solução 1
(1) Uma das relações de Girard afirma que a soma das raízes de uma equação do segundo grau é igual à razão entre o oposto do coeficiente de [tex]x[/tex] e o coeficiente de [tex]x^2[/tex], ou seja, a soma das raízes da equação [tex]ax^2+bx+c=0[/tex] é dada por [tex]\boxed{\dfrac{-b}{a}}[/tex].
(2) Uma outra relação de Girard afirma que o produto das raízes de uma equação do segundo grau é igual à razão entre o seu termo independente [tex]c[/tex] e o seu coeficiente de [tex]x^2[/tex], o que implica dizer que o produto das raízes da equação [tex]ax^2+bx+c=0[/tex] é dado por [tex]\boxed{\dfrac{c}{a}}[/tex].
(Para conhecer um pouco mais sobre as relações de Girard, cliquem AQUI.)
Solução 1
Observando o gráfico da função [tex]f[/tex], vemos que [tex]f(b)=f(4)=0[/tex], ou seja, os números [tex]b\, [/tex] e [tex]\, 4[/tex] são raízes da equação do segundo grau [tex]x^2+bx+c=0.[/tex]
Utilizando, então, as relações de Girard para a soma e para o produto de raízes de uma equação do segundo grau, temos:
[tex]b+4=\dfrac{-b}{1}=-b \qquad [/tex] e [tex]\qquad b \cdot 4=\dfrac{c}{1}=c\, [/tex],
de onde obtemos [tex]\boxed{b=-2}\, [/tex] e [tex]\, \boxed{c=-8}\, .[/tex]
Com isso, a expressão que define a função [tex]f[/tex] é
[tex]f(x)=x^2-2x-8[/tex];
fazendo [tex]x=8\, [/tex], segue que:
[tex]\fcolorbox{black}{#eee0e5}{$f(8)=8^2-2\cdot 8-8=40$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.

Lembretes para Solução 2
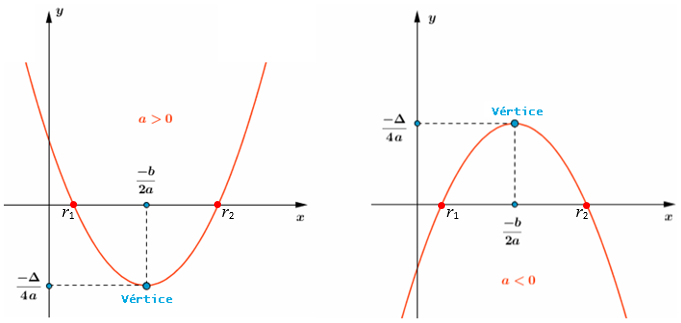
[tex]{\color{#800000}(1)}[/tex] O gráfico de uma função quadrática [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x)=ax^2+bx+c,\, a\not=0[/tex], é uma parábola com diretriz paralela ao eixo [tex]Ox[/tex], eixo de simetria paralelo ao eixo [tex]Oy[/tex], sendo sua concavidade voltada para cima se [tex]a\gt 0[/tex] e voltada para baixo se [tex]a\lt0[/tex].
[tex]{\color{#800000}(2)}[/tex] Se [tex]\Delta= b^2-4ac[/tex], as coordenadas do vértice da parábola do gráfico de [tex]h[/tex] são dadas por:
[tex]\qquad \qquad (x_v,y_v)=\bigg(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\bigg)[/tex],
sendo que [tex]x_v=\dfrac{-b}{2a}\, [/tex] e [tex]\, y_v=\dfrac{-\Delta}{4a}[/tex] indicam, respectivamente:
✓ o ponto de mínimo e o valor mínimo da função [tex]h[/tex], se a concavidade estiver voltada para cima;
✓ o ponto de máximo e o valor máximo da função [tex]h[/tex], se a concavidade estiver voltada para baixo.
Particularmente, se [tex]\Delta \gt 0[/tex], [tex]x_v[/tex] é a média entre as duas raízes de [tex]h[/tex]: [tex]x_v=\frac{r_1+r_2}{2}[/tex]
Visualizem as informações fornecidas no lembrete [tex]{\color{#800000}(2)}[/tex], se [tex]\Delta \gt 0[/tex],
clicando no botão abaixo.
Solução 2
Observando o gráfico da função dado no problema, vemos que os números [tex]b\, [/tex] e [tex]\, 4[/tex] são raízes (ou os zeros) da função [tex]f[/tex] e, como a coordenada [tex]x_v[/tex] do vértice do gráfico de [tex]f[/tex] é a média dessas raízes, segue que
[tex]\qquad x_v=\dfrac{b+4}{2}[/tex]
[tex]\qquad \dfrac{-b}{2}=\dfrac{b+4}{2}[/tex]
[tex]\qquad -b=b+4[/tex]
[tex]\qquad -2b=4[/tex]
e, então, [tex]\boxed{b=-2}\, .[/tex]
Dessa forma, podemos reescrever a expressão que define [tex]f[/tex] como [tex]\boxed{f(x)=x^2-2x+c}\, .[/tex]
Mas sabemos que [tex]\, 4[/tex] é uma raiz (ou o zero) da função [tex]f[/tex], assim:
[tex]\qquad f(4)=0[/tex]
[tex]\qquad 4^2-2\cdot 4+c=0[/tex]
[tex]\qquad 16-8+c=0[/tex]
e, então [tex]\boxed{c=-8}\, .[/tex]
Dessa forma, a expressão que define a função [tex]f[/tex] é [tex]\boxed{f(x)=x^2-2x-8}[/tex] e, portanto, [tex]\fcolorbox{black}{#eee0e5}{$f(8)=8^2-2\cdot 8-8=40$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |