✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
De cada uma das três pontas de um triângulo equilátero de lados medindo [tex]8\, cm[/tex], foram recortados três pequenos triângulos equiláteros de mesmo tamanho, de modo que a soma dos perímetros dos três triângulos pequenos fosse igual ao perímetro do hexágono resultante (que aparece colorido na figura).
Qual o comprimento, em centímetros, de cada lado dos triângulos pequenos que foram recortados?
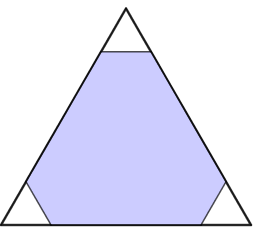A figura não é proporcional aos dados do problema.
Solução
O comprimento dos lados do triângulo equilátero original era [tex]8\, cm\, [/tex]. Assim, se [tex]l[/tex] for o comprimento dos lados dos triângulos menores, então os lados maiores do hexágono colorido na figura de referência abaixo terão comprimento [tex]\boxed{8-2l}[/tex] cada.
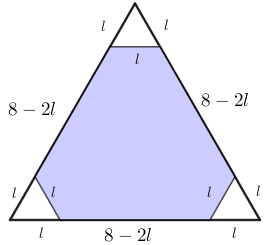
Como a soma dos perímetros dos três triângulos pequenos é igual ao perímetro do hexágono, segue que:
[tex]\qquad 3\times(l+l+l)=3l+3\times(8-2l)[/tex]
[tex]\qquad 9l=3l+24-6l[/tex]
[tex]\qquad 12l=24[/tex]
[tex]\qquad \boxed{l=\dfrac{24}{12}=2}\, .[/tex]
Dessa forma, o comprimento de cada lado dos triângulos pequenos que foram recortados é [tex]\, \fcolorbox{black}{#E6E6FA}{$2\, cm$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Nível B – Questão Média
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |