✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)
Para sua festa de aniversário, Jamile alugou um dos salões de uma empresa que organiza eventos.
Esse salão tem a forma de um [tex]\textcolor{#d38eff}{\text{T}} \, [/tex], conforme mostrado na figura abaixo, e oferece uma divisória móvel, representada pelo segmento [tex]NM[/tex], que aumenta e reduz o ambiente, permitindo várias opções de tamanho para o salão. (As linhas [tex]NM[/tex] e [tex]FE [/tex] são paralelas.)
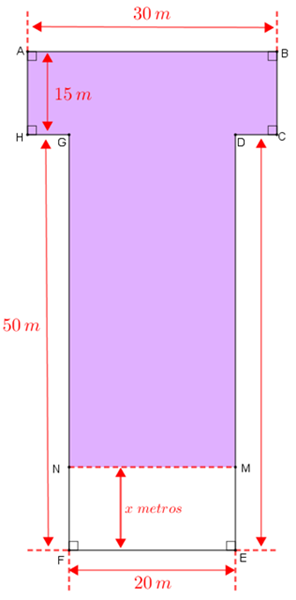
Para iniciar o planejamento da decoração de sua festa, Jamile precisa saber o perímetro do polígono [tex]\textcolor{#d38eff}{ABCDMNGH} \, .[/tex]
Para ajudá-la, vamos denotar por [tex] x[/tex] o comprimento em metros do segmento [tex] FN[/tex], com [tex]0 \leqslant x \leqslant 50[/tex], denotar por [tex] f(x) [/tex] o perímetro em questão e fazer alguns cálculos.
Assim:
(a) Expresse [tex] f(x)[/tex] em função de [tex] x[/tex].
(b) Calcule [tex]f(0)[/tex] e [tex]f(50)[/tex].
(c) Descreva o salão quando [tex]x=0[/tex] e quando [tex] x=50[/tex].
(d) Esboce o gráfico da função [tex] f[/tex] que fornece o perímetro do polígono [tex]ABCDMNGH[/tex].
Solução
O perímetro [tex]f(x)[/tex] do polígono [tex]\textcolor{#d38eff}{ABCDMNGH}[/tex] depende do comprimento [tex] x[/tex] do segmento [tex] FN[/tex], como a própria notação [tex]f(x)[/tex] indica. Na figura a seguir, explicitamos todas as medidas, em metros, dos segmentos que definem o polígono, com exceção da medida dos segmentos [tex]CD[/tex] e [tex]GH[/tex].
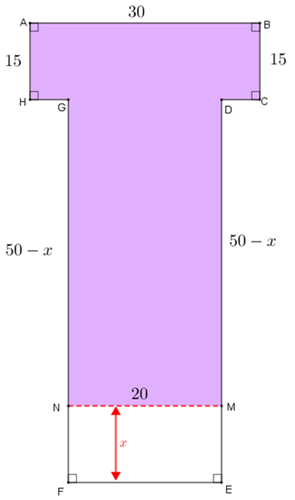
(a) Analisando a figura, percebemos que a soma dos comprimentos [tex]CD[/tex] e [tex]GH[/tex] é [tex]30-20=10 \, m[/tex]; assim, o perímetro [tex]f(x)[/tex] em metros é dado por:
[tex]\qquad \qquad f(x)=30+15+(50-x)+20+(50-x)+15+10[/tex]
[tex]\qquad \qquad \, \fcolorbox{black}{#eee0e5}{$f(x)=190-2x$} \, .[/tex]
(b) Como [tex]f(x)=190-2x \, [/tex], concluímos que:
- [tex]f(0)=190-2\cdot 0 \, [/tex]
- [tex]f(50)=190-2\cdot 50 \, [/tex]
[tex]f(0)=190 \, [/tex]
[tex]f(50)=90 \, [/tex]
(c) Observe a figura a seguir.
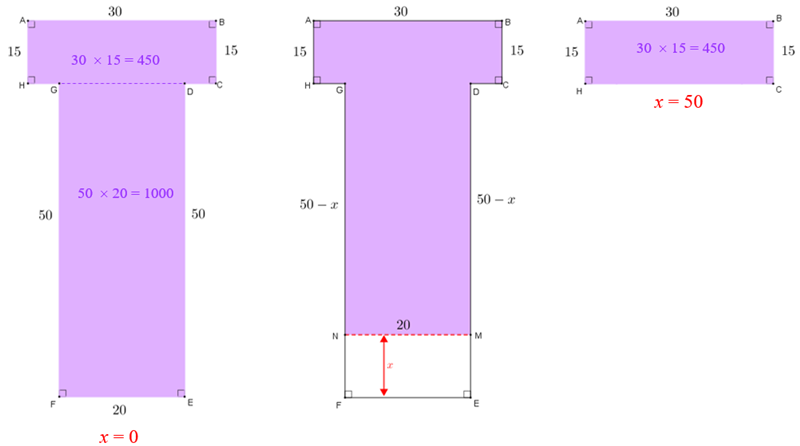
- Quando [tex]x=0[/tex], podemos ver que o polígono [tex]ABCDMNGH[/tex] coincide com o polígono [tex]ABCDEFGH[/tex] e a divisória móvel permite o salão com a maior área possível: [tex]30 \cdot 15+20 \cdot 50=1450 \, m^2.[/tex]
- Quando [tex]x=50[/tex], vemos que o polígono [tex]ABCDMNGH[/tex] coincide com o polígono [tex]ABCDGH[/tex] e a divisória móvel permite o salão com a menor área possível: [tex]30 \cdot 15=450 \, m^2.[/tex]
(d) A função que define o perímetro pode ser assim definida:
[tex]\begin{align*}f:& \, [0,50] \rightarrow [90,190]\\
&f(x)=190-2x
\end{align*}[/tex].
Neste caso, o esboço do gráfico da função [tex]f[/tex] ficaria assim:
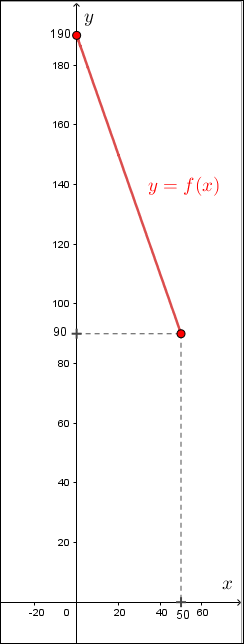
Na verdade, a função pode ser definida como
[tex]\begin{align*}f:& \, [0,50] \rightarrow T\\
&f(x)=190-2x
\end{align*}\;\;[/tex] , sendo [tex]T[/tex] qualquer subconjunto de [tex]\mathbb{R}[/tex] tal que [tex][90,190] \subset T.[/tex]
Se [tex]T=[90,190][/tex], conforme definimos, a função [tex]f[/tex] é o que chamamos uma bijeção.
No caso de [tex][90,190] \subsetneqq T[/tex] (contido, mas diferente), teremos uma função injetora, mas não sobrejetora.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
