✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F.) (Nível: Médio)
Um retângulo foi dividido em quatro retângulos menores, traçando-se linhas paralelas aos seus lados. Dos quatro retângulos formados, foram dados os perímetros de três, conforme mostra a figura abaixo.
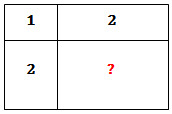Observação: A figura não está em escala.
Qual é o perímetro do quarto retângulo?
Solução
Indiquemos as medidas dos lados dos retângulos em questão por [tex]a, \, b, \, y, \, x[/tex], conforme figura a seguir.
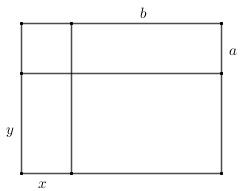
De acordo com os dados do problema, temos que:
- [tex]2b+2a=2;[/tex]
- [tex]2x+2y=2;[/tex]
- [tex]2a+2x=1.[/tex]
Dessa forma, multiplicando-se as equações acima por [tex]2, \, [/tex] [tex]2, \, [/tex] e [tex] \, \frac{1}{2}, \, [/tex] respectivamente, segue que:
- [tex]b+a=1;\qquad \color{#800000}(i)[/tex]
- [tex]x+y=1;\qquad \color{#800000}(ii)[/tex]
- [tex]a+x=\frac{1}{2}.\qquad \color{#800000}(iii)[/tex]
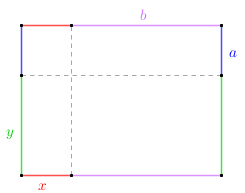
Como o perímetro do quarto retângulo é [tex]P=2b+2y[/tex], basta calcularmos [tex]b+y[/tex].
Vamos lá!
Inicialmente, perceba que:
[tex]\qquad b+y=\left(b+a-a\right)+\left(y+x-x\right),[/tex]
logo,
[tex]\qquad b+y=\left(b+a\right)+\left(x+y\right)-\left(a+x\right).[/tex]
Agora, da soma das equações [tex]\color{#800000}(i)[/tex], [tex]\color{#800000}(ii)[/tex] e [tex]\color{#800000}(iii)[/tex], segue que:
[tex]\qquad b+y=1+1-\dfrac{1}{2}[/tex]
[tex]\qquad b+y=\dfrac{3}{2},[/tex]
e, assim, o perímetro do quarto retângulo é
[tex] \qquad \fcolorbox{black}{#eee0e5}{$ \, P=2b+2y=2(b+y)=2 \times \dfrac{3}{2}=3 \, unidades \, de \, comprimento.$}[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |