✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)
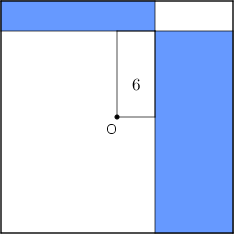
(Adaptado da Olimpíada Mexicana de Matemática) Na figura vemos um quadrado de lados [tex]8 \, cm[/tex], cujo centro é o ponto [tex]O[/tex], e um retângulo central cuja área é [tex]6 \, cm^2[/tex].
Qual é a área em [tex]dm^2[/tex] da região destacada em azul? E em [tex]mm^2[/tex]?
Solução
A partir do ponto [tex]O[/tex], vamos dividir de forma simétrica o quadrado externo em retângulos, conforme indicamos na próxima figura. Indicaremos por [tex]a \, , \, b \, ,c \, [/tex] a área em centímetros dos novos retângulos, conforme mostra a mesma figura.
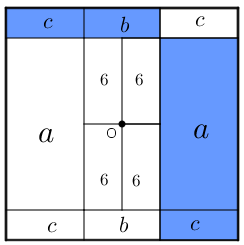
Perceba que, dessa forma, a área em [tex]cm^2[/tex] da região destacada em azul será [tex]A=a+b+2c.[/tex]
Por outro lado, como os lados do quadrado externo medem [tex]8 \, cm[/tex], então
[tex]\qquad 2a+2b+4c+4\times 6=8^2[/tex]
[tex]\qquad 2a+2b+4c+24=64[/tex]
[tex]\qquad 2a+2b+4c=64-24[/tex]
[tex]\qquad 2a+2b+4c=40[/tex]
[tex]\qquad a+b+2c=20[/tex]
[tex]\qquad A=20[/tex]
e, assim, a região destacada em azul é [tex]\boxed{20 \, cm^2}.[/tex]
Para finalizarmos o problema, precisamos converter [tex]20 \, cm^2 \, [/tex] em [tex]dm^2 \, [/tex] e em [tex]mm^2.[/tex]
O esqueminha abaixo pode ajudar!
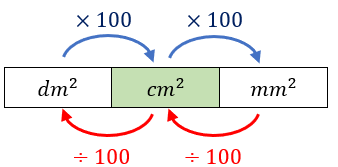
- Área da região destacada em azul em [tex]dm^2:[/tex]
[tex]\qquad 20 \, cm^2 \div 100 \longmapsto\fcolorbox{black}{#eee0e5}{$0,2 \, dm^2$} \, .[/tex] - Área da região destacada em azul em [tex]mm^2:[/tex]
[tex]\qquad 20 \, cm^2 \times 100 \longmapsto \fcolorbox{black}{#CAE1FF}{$2\,000 \, mm^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Nível B – Questão Fácil
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
