.Problema para ajudar na escola: Um gráfico transformado em três

✏ Link do problema para dispositivos da Apple.

Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Difícil)

O gráfico abaixo é parte de uma reportagem sobre a folha de pagamento do funcionalismo federal, publicada no jornal Folha de São Paulo, em 16/11/18.

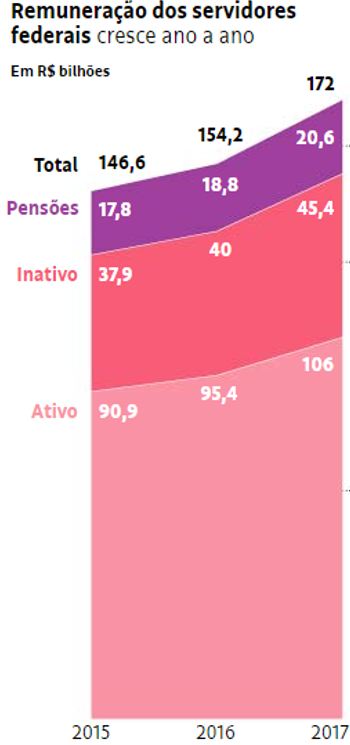
Utilize os dados sobre a remuneração dos servidores federais mostrados no gráfico acima e construa três gráficos de setores mostrando, por ano, as remunerações das categorias.

Solução

(1) Ano de [tex]2015[/tex]
Os dados relativos às remunerações das três categorias de servidores federais no ano de [tex]2015[/tex] são os mostrados na tabela a seguir e totalizam [tex]R\$\,146,6[/tex] bilhões.

[tex]\begin{array}{|c|c|c|}
\hline
\text{Ativos} & \text{Inativos} & \text{Pensões}\\
\hline
\text{R\$ 90,9 bilhões} & \text{R\$ 37,9 bilhões} & \text{R\$ 17,8 bilhões}\\
\hline
\end{array}[/tex]
Tabela 1

Para construir o gráfico de setores (“gráfico de pizza”) correspondente aos dados de [tex]2015[/tex], devemos encontrar uma relação diretamente proporcional entre eles e as áreas de cada setor circular (as fatias da pizza) a eles correspondentes.
Vamos então determinar as medidas dos ângulos que definirão cada setor circular. Para isso, levaremos em conta que a área completa da região circular do gráfico de setores (que equivale ao total pago) corresponde a um ângulo total de [tex]360^\circ [/tex]. Dessa forma, criaremos a seguinte relação: [tex]146,6[/tex] bilhões de reais está para [tex]360^\circ [/tex]. Com base nessa relação, determinaremos as respectivas medidas dos ângulos, resolvendo regrinhas de três simples.

Ativos

[tex]\begin{array}{c c c}
\;146,6 & \text{———-} & 360^\circ \;\\
\;90,9 & \text{———-} & x_a^\circ \;\end{array}[/tex]

Dessa forma, obtemos que
[tex]\;90,9 \times 360= 146,6\, x_a[/tex],
donde:
[tex]\;x_a=\dfrac{32724}{146,6}\approx 223,2[/tex].

Inativos

[tex]\begin{array}{c c c}
\; 146,6 & \text{———-} & 360^\circ \;\\
\;37,9 & \text{———-} & x_i^\circ \;\end{array}[/tex]

Dessa forma, obtemos que
[tex]\;37,9 \times 360= 146,6\, x_i[/tex],
donde:
[tex]\;x_i=\dfrac{13644}{146,6}\approx 93,1[/tex].

Pensões

[tex]\begin{array}{c c c}
\;146,6 & \text{————} & 360^\circ \;\\
\;17,8 & \text{————} & x_p^\circ \;\end{array}[/tex]

Dessa forma, obtemos que
[tex]\;17,8 \times 360= 146,6\, x_p[/tex],
donde:
[tex]\;x_p=\dfrac{6408}{146,6}\approx 43,7[/tex].

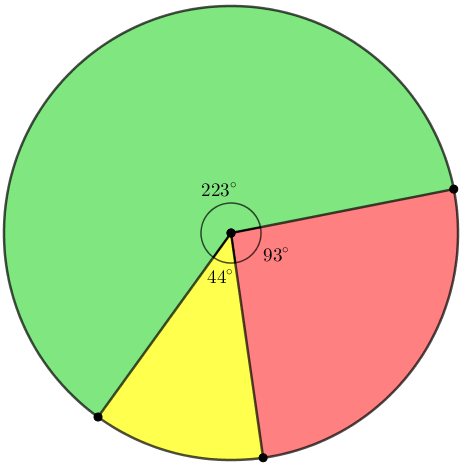
Assim, no gráfico que iremos traçar,

o setor circular que corresponderá ao gasto com servidores ativos é definido por um ângulo de [tex]\, \fcolorbox{black}{#9AFF9A}{$223^{\circ}$}\, [/tex], aproximadamente;
o setor circular que corresponderá ao gasto com servidores inativos é definido por um ângulo de [tex]\, \fcolorbox{black}{#f99}{$93^{\circ}$}\, [/tex], aproximadamente;
o setor circular que corresponderá ao gasto com pensões é definido por um ângulo de [tex]\, \fcolorbox{black}{#FFFF00}{$44^{\circ}$}\, [/tex], aproximadamente.

As medidas em graus foram aproximadas por números inteiros, para facilitar a construção dos ângulos.

Nesse tipo gráfico, não é usual a exibição das medidas dos ângulos utilizados na construção dos setores. O que identifica cada setor são os números percentuais correspondentes aos valores parciais que definem cada um. Vamos então calcular as porcentagens relativas a cada número da Tabela 1. Para isso, utilizaremos o valor de [tex]146,6[/tex] bilhões de reais como o todo ([tex]100\%[/tex]) e calcularemos o percentual correspondente aos três valores da tabela por meio de regrinhas de três simples.

Ativos

[tex]\begin{array}{c c c}
\,146,6 & \text{———-} & 100\% \,\\
\,90,9 & \text{———-} & y_a\% \,\end{array}[/tex]

Dessa forma, obtemos que
[tex]\,100\times 90,9= 146,6\, y_a[/tex],
donde:
[tex]\,y_a=\dfrac{9090}{146,6}\approx 62[/tex].

Inativos

[tex]\begin{array}{c c c}
\,146,6 & \text{———-} & 100\% \,\\
\,37,9 & \text{———-} & y_i\% \,\end{array}[/tex]

Dessa forma, obtemos que
[tex]\quad 100\times 37,9= 146,6\, y_i[/tex],
donde:
[tex]\quad y_i=\dfrac{3790}{146,6}\approx 25,9[/tex].

Pensões

[tex]\begin{array}{c c c}
\;146,6 & \text{———-} & 100\% \;\\
\;17,8 & \text{———-} & y_p\% \;\end{array}[/tex]

Dessa forma, obtemos que
[tex]\;100\times 17,8 = 146,6\, y_p[/tex],
donde:
[tex]\;y_p=\dfrac{1780}{146,6}\approx 12,1[/tex].

Assim, do total pago aos servidores federais em [tex]2015[/tex], aproximadamente

[tex]\, \fcolorbox{black}{#9AFF9A}{$62\%$} [/tex] foi gasto com servidores ativos; [tex]\, \fcolorbox{black}{#f99}{$25,9\%$} [/tex] foi gasto com servidores inativos;[tex]\, \fcolorbox{black}{#FFFF00}{$12,1\%$} [/tex] foi gasto com pensões.

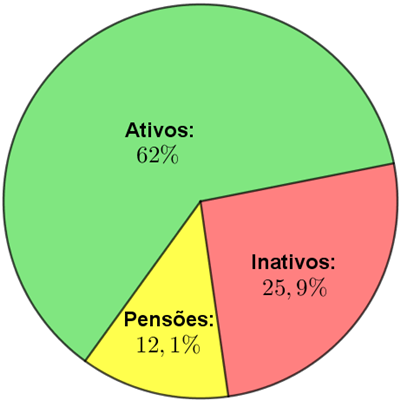
Gráfico de setores relativo ao ano de 2015

(2) Ano de [tex]2016[/tex]
As justificativas deste item são as mesmas apresentadas no item (1); assim, aqui, apresentaremos apenas os cálculos.
Os dados relativos às remunerações das três categorias de servidores federais no ano de [tex]2016[/tex] são os mostrados na tabela abaixo e totalizam [tex]R\$\, 154,2[/tex] bilhões.

[tex]\begin{array}{|c|c|c|}
\hline
\text{Ativos} & \text{Inativos} & \text{Pensões}\\
\hline
\text{R\$ 95,4 bilhões} & \text{R\$ 40 bilhões} & \text{R\$ 18,8 bilhões}\\
\hline
\end{array}[/tex]
Tabela 2

Para construir o gráfico de setores (“gráfico de pizza”) correspondente aos dados de [tex]2016[/tex], vamos inicialmente determinar as medidas dos ângulos que irão definir cada setor circular. Para tal, consideraremos que a área completa da região circular do gráfico de setores corresponde a um ângulo total de [tex]360^\circ [/tex]. Dessa forma, criaremos a seguinte relação: [tex]154,2[/tex] bilhões de reais está para [tex]360^\circ [/tex]. Vejam as respectivas regras de três simples.

Ativos

[tex]\begin{array}{c c c}
\;154,2 & \text{———-} & 360^\circ \;\\
\;95,4 & \text{———-} & x_a^\circ \;\end{array}[/tex]

Dessa forma, obtemos que
[tex]\;95,4 \times 360= 154,2\, x_a[/tex],
donde:
[tex]\;x_a=\dfrac{34344}{154,2}\approx 222,7[/tex].

Inativos

[tex]\begin{array}{c c c}
\;154,2 & \text{———-} & 360^\circ \;\\
\;40 & \text{———-} & x_i^\circ \;\end{array}[/tex]

Dessa forma, obtemos que
[tex]\;40 \times 360= 154,2\, x_i[/tex],
donde:
[tex]\;x_i=\dfrac{144000}{154,2}\approx 93,4[/tex].

Pensões

[tex]\begin{array}{c c c}
\;154,2 & \text{———-} & 360^\circ \;\\
\;18,8 & \text{———-} & x_p^\circ \;\end{array}[/tex]

Dessa forma, obtemos que
[tex]\;18,8 \times 360= 154,2\, x_p[/tex],
donde:
[tex]\;x_p=\dfrac{6768}{154,2}\approx 43,9[/tex].

Assim, no gráfico que iremos traçar,

o setor circular que corresponderá ao gasto com servidores ativos é definido por um ângulo de [tex]\, \fcolorbox{black}{#9AFF9A}{$223^{\circ}$}\, [/tex], aproximadamente;
o setor circular que corresponderá ao gasto com servidores inativos é definido por um ângulo de [tex]\, \fcolorbox{black}{#f99}{$93^{\circ}$}\, [/tex], aproximadamente;
o setor circular que corresponderá ao gasto com pensões é definido por um ângulo de [tex]\, \fcolorbox{black}{#FFFF00}{$44^{\circ}$}\, [/tex], aproximadamente.

Ao aproximarmos as medidas como no item (1), percebemos que, embora o total pago aos servidores em [tex]2016[/tex] tenha aumentado de [tex]146,6[/tex] para [tex]154,2[/tex] bilhões de reais, a distribuição do valor pago entre as três categorias permaneceu praticamente a mesma.
Dessa forma, o gráfico de setores relativo ao ano de [tex]2016[/tex] com a indicação percentual é o mesmo de [tex]2015[/tex].

Gráfico de setores relativo ao ano de 2016

(3) Ano de [tex]2017[/tex]
Também neste item, as justificativas são as mesmas apresentadas no item (1). Mais uma vez, apresentaremos apenas os cálculos.
Inicialmente, apresentamos os dados relativos às remunerações das três categorias de servidores federais no ano de [tex]2017[/tex], e que totalizam [tex]R\$\, 172[/tex] bilhões, na tabela abaixo.

[tex]\begin{array}{|c|c|c|}
\hline
\text{Ativos} & \text{Inativos} & \text{Pensões}\\
\hline
\text{R\$ 106 bilhões} & \text{R\$ 45,4 bilhões} & \text{R\$ 20,6 bilhões}\\
\hline
\end{array}[/tex]
Tabela 3

A construção do gráfico de setores correspondente aos dados de [tex]2017[/tex] também será iniciada com a determinação das medidas dos ângulos que irão definir cada um dos três setores circulares. Mais uma vez, consideraremos que a área do círculo que definirá o gráfico de setores corresponde a um ângulo total de [tex]360^\circ [/tex]. Aqui, trabalharemos com a seguinte relação: [tex]172[/tex] bilhões de reais está para [tex]360^\circ [/tex]. Vejam as respectivas regras de três simples.

Ativos

[tex]\begin{array}{c c c}
\;172& \text{———-} & 360^\circ \;\\
\;106 & \text{———-} & x_a^\circ \;\end{array}[/tex]

Dessa forma, obtemos que
[tex]\;106\times 360= 172\, x_a[/tex],
donde:
[tex]\;x_a=\dfrac{38160}{172}\approx 221,9[/tex].

Inativos

[tex]\begin{array}{c c c}
\;172& \text{———-} & 360^\circ \;\\
\;45,4 & \text{———-} & x_i^\circ \;\end{array}[/tex]

Dessa forma, obtemos que
[tex]\quad 45,4 \times 360= 172\, x_i[/tex],
donde:
[tex]\quad x_i=\dfrac{16344}{172}\approx 95[/tex].

Pensões

[tex]\begin{array}{c c c}
\;172& \text{———-} & 360^\circ \;\\
\;20,6 & \text{———-} & x_p^\circ \;\end{array}[/tex]

Dessa forma, obtemos que
[tex]\quad 20,6 \times 360= 172\, x_p[/tex],
donde:
[tex]\;x_p=\dfrac{7416}{172}\approx 43,1[/tex].

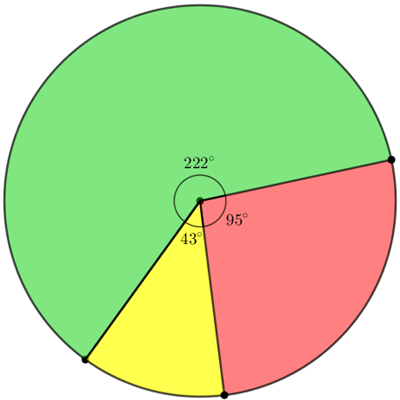
Assim, neste último gráfico,

o setor circular que corresponderá ao gasto com servidores ativos é definido por um ângulo de [tex]\, \fcolorbox{black}{#9AFF9A}{$222^{\circ}$}\, [/tex], aproximadamente;
o setor circular que corresponderá ao gasto com servidores inativos é definido por um ângulo de [tex]\, \fcolorbox{black}{#f99}{$95^{\circ}$}\, [/tex], aproximadamente;
o setor circular que corresponderá ao gasto com pensões é definido por um ângulo de [tex]\, \fcolorbox{black}{#FFFF00}{$43^{\circ}$}\, [/tex], aproximadamente.

Novamente aproximamos as medidas em graus dos ângulos, para facilitar a construção.

Vamos calcular agora as porcentagens relativas aos números da Tabela 3. Utilizaremos o valor de [tex]172[/tex] bilhões de reais como [tex]100\%[/tex] e calcularemos o percentual correspondente aos três valores da tabela por meio de regras de três simples.

Ativos

[tex]\begin{array}{c c c}
\;172 & \text{————–} & 100\% \;\\
\;106 & \text{————–} & y_a\% \;\end{array}[/tex]

Dessa forma, obtemos que
[tex]\;100\times 106= 172 \, y_a[/tex],
donde:
[tex]\;y_a=\dfrac{10600}{172 }\approx 61,6[/tex].

Inativos

[tex]\begin{array}{c c c}
\;172 & \text{———-} & 100\% \;\\
\;45,4 & \text{———-} & y_i\% \;\end{array}[/tex]

Dessa forma, obtemos que
[tex]\;100\times 45,4= 172 \, y_i[/tex],
donde:
[tex]\;y_i=\dfrac{4540}{172 }\approx 26,4[/tex].

Pensões

[tex]\begin{array}{c c c}
\;172 & \text{———-} & 100\% \;\\
\;20,6& \text{———-} & y_p\% \;\end{array}[/tex]

Dessa forma, obtemos que
[tex]\;100\times 20,6 = 172 \, y_p[/tex],
donde:
[tex]\;y_p=\dfrac{2060}{172 }\approx 12[/tex].

Assim, do total pago aos servidores federais em [tex]2017[/tex], aproximadamente

[tex]\, \fcolorbox{black}{#9AFF9A}{$61,6\%$} [/tex] foi gasto com servidores ativos; [tex]\, \fcolorbox{black}{#f99}{$26,4\%$} [/tex] foi gasto com servidores inativos;[tex]\, \fcolorbox{black}{#FFFF00}{$12\%$} [/tex] foi gasto com pensões.

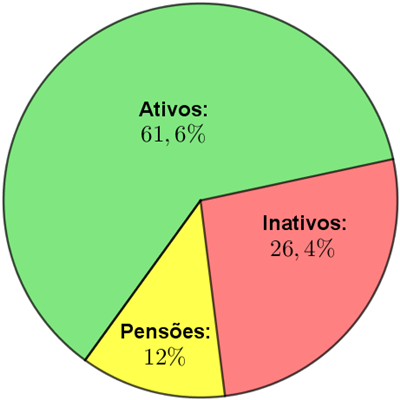
Gráfico de setores relativo ao ano de 2017

Solução elaborada pelos Moderadores do Blog.

Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo.
Você pode abrir o arquivo diretamente no seu navegador (Chrome, Edge, Firefox, Safari, entre outros), mas também pode utilizar o software gratuito Adobe Acrobat Reader.
Caso o dispositivo que você está utilizando não tenha o Acrobat Reader instalado, é só clicar AQUI para fazer o download adequado ao seu dispositivo.

Arquivo