Problema
(Indicado a partir do 9º ano do E. F.)
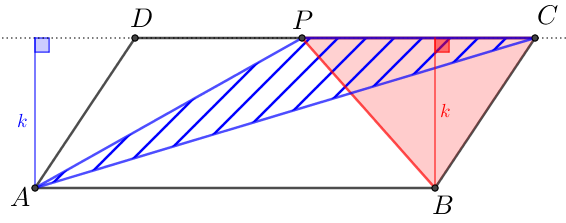
(XXXIII OPM, 2015) No paralelogramo [tex]ABCD[/tex] da figura abaixo,
- [tex]P[/tex] é um ponto do segmento [tex]\overline{DC}[/tex];
- o ponto [tex]Q[/tex] é a interseção da diagonal [tex]\overline{AC} [/tex] com a reta que passa por [tex]P[/tex] e é paralela ao segmento [tex]\overline{AD}[/tex].
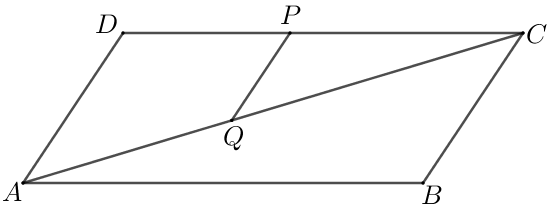
Figura não proporcional aos dados do problema
Sabendo que a área do triângulo [tex]PBQ [/tex] é [tex]2 \, cm^2[/tex] e a área do triângulo [tex]ABP [/tex] é [tex]6 \, cm^2[/tex], determine as áreas em [tex]cm^2[/tex] dos triângulos [tex]ADC \, [/tex] e [tex] \, PBC[/tex].
Notações:
– Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY[/tex].
– Denotaremos a área de um triângulo [tex]XYZ[/tex], por exemplo, por [tex][XYZ].[/tex]

AJUDA
Definição: Um quadrilátero convexo cujos lados opostos são paralelos é denominado paralelogramo.
Propriedades:
(1) Lados opostos de um paralelogramo são congruentes, ou seja, têm mesma medida.
(2) Caso de Semelhança A.A. (ângulo – ângulo): Se dois ângulos de um triângulo são congruentes a dois ângulos de outro triângulo, então estes triângulos são semelhantes.
(3) A razão entre as áreas de dois triângulos semelhantes é o quadrado da razão de semelhança.
Solução
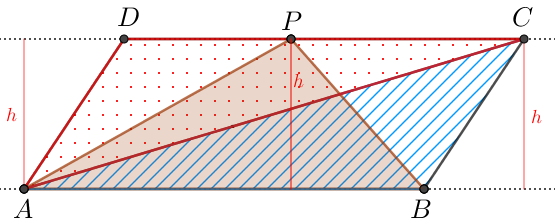
- Ao prolongarmos os segmentos [tex]\overline{DC}[/tex] e [tex]\overline{AB}[/tex], podemos observar que os triângulos [tex]ACD \, [/tex], [tex] \, ACB \, [/tex] e [tex] \, ABP \, [/tex] têm alturas com o mesmo comprimento [tex]\textcolor{red}{h}[/tex]. Dessa forma, esses triângulos têm a mesma área, já que as bases relativas às respectivas alturas de comprimento [tex]\textcolor{red}{h}[/tex] têm a mesma medida, devido à Propriedade (1) da AJUDA.
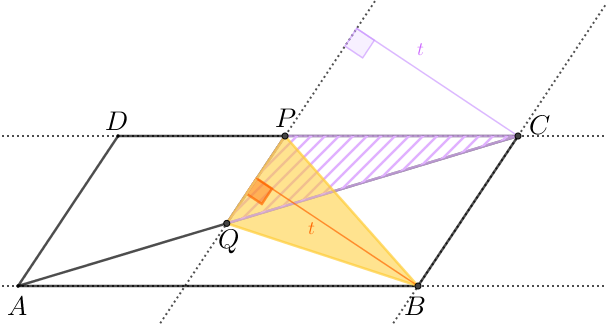
Com isso, como a área do triângulo [tex]ABP[/tex] é [tex]6 \, cm^2[/tex], então a área do triângulo [tex]ACD \, [/tex] é também [tex] \, \boxed{6 \, cm^2} \, .[/tex] - Ao prolongarmos os segmentos [tex]\overline{PQ}[/tex] e [tex]\overline{CB}[/tex], podemos notar que os triângulos [tex]PQB \, [/tex] e [tex] \, PQC \, [/tex] têm alturas relativas à base comum [tex]\overline{PQ}[/tex] com o mesmo comprimento [tex]t[/tex], pois os segmentos [tex]\overline{PQ}[/tex] e [tex]\overline{CB}[/tex] são paralelos (hipótese do problema e Definição da AJUDA ).
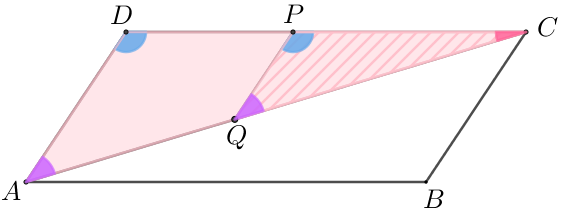
Com isso, os triângulos [tex]PQB \, [/tex] e [tex] \, PQC[/tex] têm a mesma área. Como a área do triângulo [tex]PBQ [/tex] é [tex]2 \, cm^2[/tex], a área do triângulo [tex]PQC[/tex] também será [tex]\boxed{2 \, cm^2} \, .[/tex] - Observando os triângulos [tex]DCA \, [/tex] e [tex] \, PCQ[/tex] e utilizando a Propriedade(2) da AJUDA, podemos concluir que eles são semelhantes.
- Ao prolongarmos o segmento [tex]\overline{CD}[/tex], notamos que os triângulos [tex]PCB \, [/tex] e [tex] \, PCA \, [/tex] têm alturas relativas à base comum [tex]\overline{PC}[/tex] com o mesmo comprimento [tex]k[/tex], pois os segmentos [tex]\overline{DC}[/tex] e [tex]\overline{AB}[/tex] são paralelos (Propriedade (1) da AJUDA).
Com isso, os triângulos [tex]PCB \, [/tex] e [tex] \, PCA[/tex] têm a mesma área.
Assim, pela Propriedade (3) da AJUDA, segue que:
[tex] \qquad \dfrac{[DCA]}{[PCQ]}= \dfrac{CD^2}{CP^2}\\
\, \, [/tex]
[tex] \qquad \dfrac{6}{2}= \dfrac{CD^2}{CP^2}\\
\, \, [/tex]
[tex] \qquad \left(\dfrac{CD}{CP}\right)^2=3\\
\, \, [/tex]
[tex] \qquad \dfrac{CD}{CP}=\sqrt{3}\\
\, \, [/tex]
[tex] \qquad CP=\dfrac{CD}{\sqrt{3}}.[/tex]
Finalmente, temos que:
[tex]\qquad [PBC]=[PCA]\\ \, \, [/tex]
[tex]\qquad [PBC]=\dfrac{CP \times k}{2}\\ \, \, [/tex]
[tex]\qquad [PBC]=CP \times \dfrac{k}{2}\\ \, \, [/tex]
[tex]\qquad [PBC]=\dfrac{CD}{\sqrt{3}} \times \dfrac{ k}{2}\\ \, \, [/tex]
[tex]\qquad [PBC]=\dfrac{1}{\sqrt{3}} \times \dfrac{CD \times k}{2}\\ \, \, [/tex]
[tex]\qquad [PBC]=\dfrac{1}{\sqrt{3}} \times [ACD]\\ \, \, [/tex]
[tex]\qquad [PBC]=\dfrac{1}{\sqrt{3}} \times 6\\ \, \, [/tex]
[tex]\qquad [PBC]=\dfrac{6}{\sqrt{3}}\\ \, \, [/tex]
[tex]\qquad [PBC]=\dfrac{6 \times \sqrt{3}}{3}\\ \, \, [/tex]
[tex]\qquad [PBC]=2 \, \sqrt{3} \, cm^2[/tex]
Por tudo que foi exposto, temos que as áreas dos triângulos [tex]ADC \, [/tex] e [tex] \, PBC[/tex] são [tex] \, \fcolorbox{black}{#eee0e5}{$6 \, cm^2$} \, [/tex] e [tex] \, \fcolorbox{black}{#eee0e5}{$2 \, \sqrt{3} \, cm^2$} \, [/tex], respectivamente.
Solução elaborada pelos Moderadores do Blog.
