✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Médio)
Seu João é um marceneiro muito caprichoso e gosta de fazer peças de decoração.
Ontem mesmo ele pegou um cubo de madeira, fez cortes paralelos a três de suas faces e produziu a peça mostrada na figura.
Se o volume do cubo original era [tex]2\,744 \, cm^3[/tex], qual a superfície total da peça produzida por seu João?
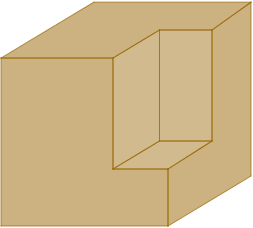
Solução
A peça de decoração manteve três faces do cubo original e tem seis outras faces que são duas a duas paralelas a uma dessas três faces originais.
Vamos nomear essas seis faces, de acordo com a próxima figura.
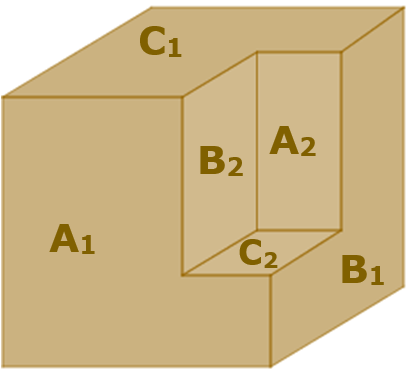
- Utilizando a figura abaixo, observe que, se unirmos as faces [tex]A_1[/tex] e [tex]A_2 \, [/tex], obtemos uma face do cubo original.
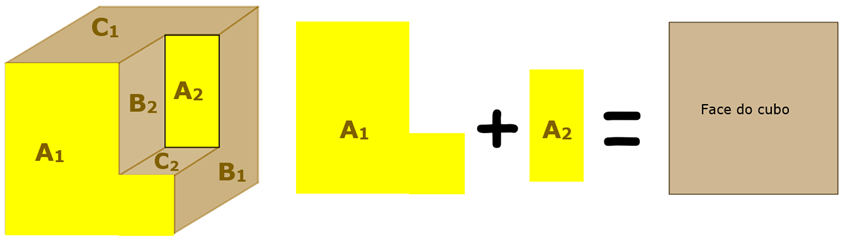
De forma análoga:
- se unirmos as faces [tex]B_1[/tex] e [tex]B_2 \, [/tex], obtemos uma face do cubo original.
- se unirmos as faces [tex]C_1[/tex] e [tex]C_2 \, [/tex], obtemos também uma face do cubo original.
Dessa forma, podemos concluir que
a superfície total da peça produzida por seu João é igual a superfície total do cubo original.
Vamos, então, calculá-la!
- Sabendo que o volume do cubo original era [tex]2\,744 \, cm^3 \, [/tex], cada lado desse cubo media [tex]\sqrt[3]{2\,744}=\boxed{14 \, cm} \, .[/tex]
Com isso, a área de cada face era [tex]14 \times 14=\boxed{196 \, cm^2} \, [/tex] e, consequentemente, a superfície total do cubo era [tex]6 \times 196=\boxed{1 \, 176 \, cm^2} \, .[/tex]
Por tudo que foi exposto, a superfície total da peça produzida por seu João é [tex] \, \fcolorbox{black}{#e1d3ba}{$1\,176 \, cm^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
