✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 2ª série do E. M.- Nível de dificuldade: Difícil)
(ITA, 2007 – Adaptado) Sejam [tex]A[/tex] um conjunto com [tex]18[/tex] elementos e [tex]D[/tex] um subconjunto de [tex]A[/tex] com [tex]8[/tex] elementos.
Quantos subconjuntos de [tex]A[/tex] que tenham [tex]8[/tex] ou menos elementos são disjuntos de [tex]D\,[/tex]?

Ajuda
✏ Combinação simples: Uma das maneiras de agruparmos elementos de um dado conjunto é escolhê-los levando-se em consideração apenas a sua natureza, sem se importar em que ordem eles foram escolhidos ou apresentados. Esse tipo de agrupamento de elementos é denominado uma Combinação simples. Particularmente, quando escolhemos [tex]r[/tex] dentre [tex]n[/tex] elementos de um conjunto dessa forma, dizemos que estamos definindo uma Combinação simples de [tex]n[/tex] elementos tomados [tex]r[/tex] a [tex]r[/tex]. A quantidade desse tipo de agrupamentos é denotada por [tex]C_{n,r}[/tex] ou [tex]C_n^r\,[/tex] e assim definida:
[tex]C_{n,r}=C_n^r=\dfrac{n!}{(n-r)!\,r!} \text{ , com } n,r\in\mathbb{N} \text{ e } r\leqslant n[/tex].
✏ Notação: Se [tex]X[/tex] for um conjunto finito, denotaremos por [tex]\#(X)[/tex] a quantidade de elementos desse conjunto.
Solução
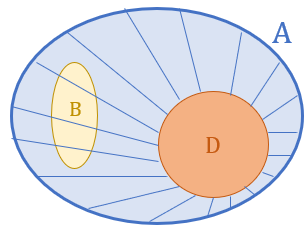
Nas condições do problema, observe que
- para um subconjunto [tex]B[/tex] de [tex]A[/tex] ser disjunto de [tex]D[/tex] necessariamente [tex]B[/tex] deve estar contido na diferença [tex]A-D.[/tex]
Assim, precisamos inicialmente contar quantos subconjuntos o conjunto [tex]A-D[/tex] tem e, em seguida, determinar quantos desses subconjuntos têm oito ou menos elementos.
Vamos lá!
- [tex]\textcolor{#800000}{(i)}[/tex] Para determinar quantos subconjuntos [tex]A-D[/tex] tem só precisamos saber a quantidade de elementos do conjunto [tex]A-D[/tex], uma vez que um conjunto com [tex]n[/tex] elementos tem [tex]2^n[/tex]subconjuntos.
- Note que o único subconjunto de um conjunto que tem a mesma quantidade de elementos do conjunto é o próprio conjunto. Assim temos um único subconjunto de [tex]A-D[/tex] com dez elementos: o [tex]A-D[/tex].
- Os subconjuntos de [tex]A-D[/tex] com nove elementos são aqueles em que um e somente um dos elementos de [tex]A-D[/tex] foi retirado. Como [tex]A-D[/tex] tem dez elementos, podemos formar dez subconjuntos distintos, eliminando em cada um exatamente um elemento do conjunto inicial.
Observe que também poderíamos contar esses subconjuntos observando que eles são as possíveis escolhas de nove elementos que podemos fazer dentre os dez elementos de [tex]A-D[/tex]. Como essas escolhas são feitas levando-se em consideração apenas a natureza dos elementos, sem se levar em consideração a ordem segundo a qual esses elementos foram escolhidos, a quantidade de escolhas é uma Combinação simples de [tex]10[/tex] elementos tomados [tex]9[/tex] a [tex]9[/tex], ou seja,
[tex]\qquad C_{10}^9=\dfrac{10!}{(10-9)!\,9!}=10[/tex].
Como [tex]D[/tex] é subconjunto de [tex]A[/tex], a diferença [tex]A-D[/tex] é o complementar de [tex]D[/tex] com relação a [tex]A[/tex] e talvez com essa nomenclatura fique mais fácil você se lembrar de que o número de elementos de [tex]A-D[/tex] é a diferença entre o número de elementos de [tex]A[/tex] e o número de elementos de [tex]D[/tex].
Em símbolos, se [tex]m[/tex] for o número de elementos de [tex]A-D[/tex], então
[tex]\qquad \qquad m=\#\left(A-D\right)=\#\left(A\right)-\#\left(D\right)[/tex].
Dessa forma, de acordo com os dados do problema, segue que:
[tex]\qquad \qquad m=\#\left(A\right)-\#\left(D\right)=18-8=10[/tex]
e, portanto, [tex]A-D[/tex] tem [tex]2^{10}[/tex] subconjuntos.
[tex]\textcolor{#800000}{(ii)}[/tex] Desses [tex]2^{10}[/tex] subconjuntos de [tex]A-D[/tex] nos interessam apenas aqueles que têm oito elementos ou menos. Assim, devemos excluir desses [tex]2^{10}[/tex] subconjuntos aqueles que têm dez elementos e também os que têm nove elementos.
Assim, o conjunto [tex]A-D[/tex] tem [tex]\boxed{1+10=11}[/tex] subconjuntos com dez ou nove elementos.
De [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(ii)}[/tex], concluímos que [tex]A[/tex] tem [tex]\,\fcolorbox{black}{#eee0e5}{$2^{10}-11=1\,013$}\,[/tex] subconjuntos disjuntos de [tex]D[/tex] com oito ou menos elementos.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
