✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
Abigail pegou os lápis de cor da sua tia e fez um desenho em uma folha de papel quadriculado por quadradinhos de lados com comprimentos 2 cm.
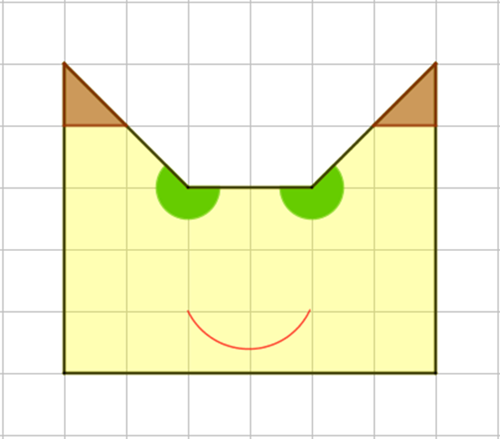
(a) Qual a área do papel que foi colorida de marrom?
(b) Se os olhos do bichinho foram feitos com um disco de diâmetro 2 cm, qual a área do papel que foi colorida de verde?
(c) Desprezando-se a espessura da boca do bichinho, qual a área do papel que foi colorida de amarelo?
Solução
Observamos, inicialmente, que a área de cada quadradinho do papel quadriculado que a Abigail utilizou é de [tex]\boxed{A_q=2^2=4 \, cm^2}.[/tex]
(a) A área do papel que foi colorida de marrom é a área que corresponde às duas orelhas do bichinho. Dependendo de como vemos a figura, podemos calcular a área [tex]\textcolor{#8B4513}{A_{orelha}}[/tex] de cada orelha de dois modos:
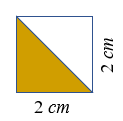
- A área corresponde à metade da área de um dos quadradinhos que quadriculam o papel:
- A área corresponde à área de um triângulo retângulo cujos lados congruentes medem [tex]2 \, cm[/tex]:
[tex]\qquad \textcolor{#8B4513}{A_{orelha}}=\dfrac{4}{2}=2\, cm^2[/tex].
[tex]\qquad \textcolor{#8B4513}{A_{orelha}}=\dfrac{base \times altura}{2}=\dfrac{2 \times 2}{2}=2\, cm^2[/tex].
De qualquer modo, a área do papel que foi colorida de marrom é dada por:
[tex]\qquad \textcolor{#8B4513}{A_{marrom}}=2 \times \textcolor{#8B4513}{A_{orelha}} [/tex]
[tex]\qquad \textcolor{#8B4513}{A_{marrom}}=2 \times 2 [/tex]
[tex]\qquad \fcolorbox{black}{#eee0e5}{$\textcolor{#8B4513}{A_{marrom}}=4 \, cm^2$} \, . [/tex]
(b) A área colorida de verde corresponde aos dois olhos do bichinho. Pelas informações do problema, cada olho foi feito a partir de um disco de diâmetro [tex]2\,cm[/tex]. A área desse disco corresponde à área de um círculo de raio [tex]1\,cm[/tex]: [tex]\boxed{A_d=\pi\times 1^2=\pi\,cm^2}.[/tex]
Observando as diagonais dos quadradinhos do papel quadriculado, podemos também calcular a área [tex]\textcolor{#2fbf2f}{A_{olho}}[/tex] de cada olho de dois modos:
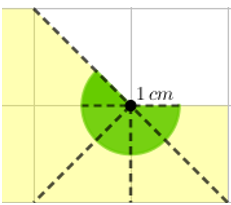
- A área do olho corresponde à "área de um semicírculo de raio [tex]1\,cm[/tex]" mais a "metade de um quarto da área de um círculo de raio [tex]1\,cm[/tex]":
- A área do olho corresponde a [tex] \frac{5}{8}[/tex] da área de um círculo de raio [tex]1\,cm[/tex]:
[tex]\qquad \textcolor{#2fbf2f}{A_{olho}}=\dfrac{A_d}{2}+\dfrac{\frac{A_d}{4}}{2}=\dfrac{\pi}{2}+\dfrac{\pi}{8}=\dfrac{5\pi}{8}\,cm^2 \, .[/tex]
[tex]\qquad \textcolor{#2fbf2f}{A_{olho}}=\dfrac{5}{8}A_d=\dfrac{5\pi}{8}\,cm^2 \, .[/tex]
Portanto, a área do papel colorida de verde é:
[tex]\qquad \textcolor{#2fbf2f}{A_{verde}}=2 \times \textcolor{#2fbf2f}{A_{olho}} [/tex]
[tex]\qquad \textcolor{#2fbf2f}{A_{verde}}=2 \times \dfrac{5\pi}{8} [/tex]
[tex]\qquad \fcolorbox{black}{#eee0e5}{$\textcolor{#2fbf2f}{A_{verde}}=\dfrac{5\pi}{4} \, cm^2 \approx 3,9\,cm^2$} \, . [/tex]
(c) A área colorida de amarelo é a diferença entre a área azul, [tex]\textcolor{#6699ff}{A_{azul}}[/tex], mostrada na imagem a seguir, e a área verde, [tex] \textcolor{#2fbf2f}{A_{verde}}[/tex], que já conhecemos.
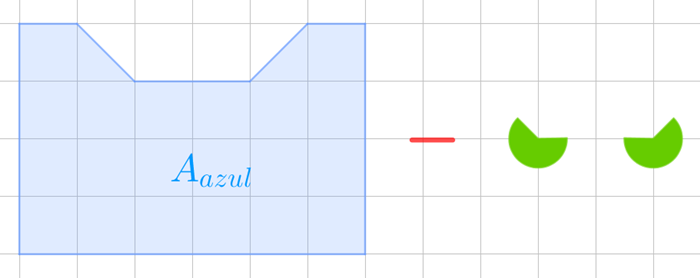
A área azul corresponde à área de [tex]21[/tex] quadradinhos, assim:
[tex]\qquad \textcolor{#6699ff}{A_{azul}}= 21 \times A_q=21 \times 4=84 \, cm^2.[/tex]
Portanto, segue que:
[tex]\qquad A_{amarela}= \textcolor{#6699ff}{A_{azul}}-\textcolor{#2fbf2f}{A_{verde}}\\
\qquad A_{amarela}= 84-\dfrac{5\pi}{4}\\
\qquad \fcolorbox{black}{#eee0e5}{$A_{amarela}= \dfrac{336-5\pi}{4}\,cm^2 \approx 80,1\, cm^2$} \, .\\
[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
