✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Médio)
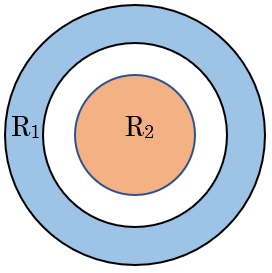
Na figura vemos três circunferências concêntricas cujos raios são [tex]7 \, , \, r \, , \, 25[/tex], com [tex]7 \lt r \lt 25 [/tex].
Determine o valor de [tex]r[/tex] para que a área da região colorida [tex]R_1[/tex] seja igual à área da região colorida [tex]R_2[/tex].
Solução
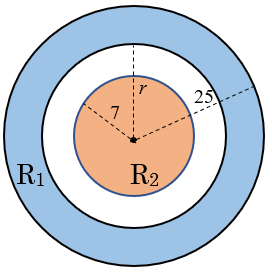 Sejam [tex]A_1 \, [/tex] e [tex] \, A_2[/tex] as respectivas áreas das regiões coloridas [tex]R_1 \, [/tex] e [tex] \, R_2 \, .[/tex]
Sejam [tex]A_1 \, [/tex] e [tex] \, A_2[/tex] as respectivas áreas das regiões coloridas [tex]R_1 \, [/tex] e [tex] \, R_2 \, .[/tex]
Assim:
[tex]\qquad A_2=7^2 \pi =49 \pi[/tex]
[tex]\qquad A_1=25^2 \pi-r^2 \pi =\left(625-r^2\right) \pi \, .[/tex]
Para que a área da região colorida [tex]R_1[/tex] seja igual à área da região colorida [tex]R_2[/tex] devemos ter:
[tex]\qquad A_1=A_2[/tex]
[tex]\qquad 49 \cancel{\pi}=\left(625-r^2\right) \cancel{\pi}[/tex]
[tex]\qquad r^2=625-49[/tex]
[tex]\qquad r^2=576[/tex]
[tex]\qquad r=\pm \, \sqrt{576}[/tex]
[tex]\qquad r=\pm \, 24 \, .[/tex]
Como [tex]r[/tex] é um comprimento, segue que [tex]r \gt 0[/tex]; logo, [tex] \, \fcolorbox{black}{#eee0e5}{$r=24$} \, [/tex] unidades de comprimento.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
