✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)
(GUELLI, O. Contando a História da Matemática: História da Equação do 2º Grau. São Paulo: Ática, 1992) Um comerciante possui uma loja e um depósito de materiais de construção.
O formato dos terrenos onde a loja e o depósito estão construídos é quadrado e juntos os dois terrenos ocupam uma área de [tex]596\, m^2[/tex]. O lado de um dos terrenos tem [tex] 6\, m[/tex] a mais que o do outro terreno.
Quais os comprimentos dos lados de cada terreno?

AJUDA
As raízes da equação do segundo grau [tex]\, \, ax^2+bx+c = 0\, \, [/tex] são dadas por
[tex]\, \, \, \, \, \, \, \, \, \, \, \, x_1 = \dfrac{-b+\sqrt{\Delta}}{2a}\, \, \, [/tex] e [tex]\, \, \, x_2 = \dfrac{-b-\sqrt{\Delta}}{2a}[/tex],
onde [tex]a,b,c[/tex] são números reais, com [tex]a\ne 0\, [/tex], e [tex]\, \Delta =b^2-4ac[/tex].
Solução
Seja [tex]x[/tex] um número real positivo e suponha que os dois terrenos quadrados tenham lados medindo [tex]x[/tex] e [tex]x+6[/tex] metros, conforme indicado na figura abaixo. Dessa forma, os terrenos têm áreas iguais a [tex]x^2[/tex] e [tex]\left(x+6\right)^2[/tex] metros quadrados.
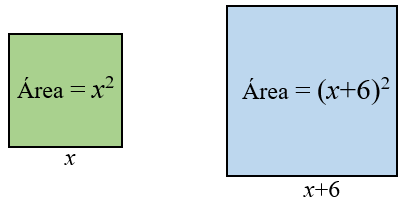
Como os dois terrenos ocupam uma área de [tex]596\, m^2[/tex] juntos, segue que:
[tex]\qquad \left(x+6\right)^2+x^2=596\\
\qquad x^2+12x+36+x^2=596\\
\qquad 2x^2+12x-560=0\\
\qquad x^2+6x-280=0. \qquad \qquad \textcolor{#800000}{(i)}[/tex]
A equação [tex]\textcolor{#800000}{(i)}[/tex] é uma equação do segundo grau cujas raízes são:
|
[tex]\, x_1 = \dfrac{-b+\sqrt{\Delta}}{2a}\, \, \, [/tex] [tex]\, x_1 = \dfrac{-b+\sqrt{b^2-4ac}}{2a}\, \, \, [/tex] [tex]\, x_1 = \dfrac{-6+\sqrt{36+1120}}{2}\, \, \, [/tex] [tex]\, x_1 = \dfrac{-6+\sqrt{1156}}{2}\, \, \, [/tex] [tex]\, x_1 = \dfrac{-6+34}{2}\, \, \, [/tex] [tex]\, x_1 = \dfrac{28}{2}\, \, .[/tex] [tex]\, \boxed{x_1 = 14}\, \, \, [/tex] |
[tex]\qquad x_2 = \dfrac{-b-\sqrt{\Delta}}{2a}[/tex] [tex]\qquad x_2 = \dfrac{-b-\sqrt{b^2-4ac}}{2a}\, \, \, [/tex] [tex]\qquad x_2 = \dfrac{-6-\sqrt{36+1120}}{2}\, \, \, [/tex] [tex]\qquad x_2 = \dfrac{-6-\sqrt{1156}}{2}\, \, \, [/tex] [tex]\qquad x_2 = \dfrac{-6-34}{2}\, \, \, [/tex] [tex]\qquad x_2 = \dfrac{-40}{2}\, \, \, [/tex] [tex]\qquad \boxed{x_2 = -20}\, \, .[/tex] |
Para efeito do problema, [tex]x[/tex] é um número real positivo, logo a raiz [tex] x_2[/tex] não é conveniente. Portanto, [tex]\, \boxed{x=14}\, [/tex] e, consequentemente, os comprimentos dos lados dos terrenos são [tex]\, \fcolorbox{black}{#eee0e5}{$14\, m$}\, [/tex] e [tex]\, \fcolorbox{black}{#eee0e5}{$20\, m$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Um applet para ajudar
Você pode utilizar o applet abaixo para visualizar vários pares de quadrados tais que o lado de um deles tem 6 metros a mais que o do outro e, com isso, visualizar a geometria e a solução do problema.
Instruções:
(1) Espere o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Mova horizontalmente o ponto identificado como [tex]\textcolor{#0000FF}{Lado_m}[/tex] para alterar diretamente a medida dos lados do quadrado menor e, consequentemente, a medida do quadrado maior.
(3) Para movimentar o ponto [tex]\textcolor{#0000FF}{Lado_m}[/tex], clique sobre ele com o botão esquerdo do mouse, mantenha o mouse pressionado e faça o movimento. (Se você estiver utilizando um celular ou um tablet, toque levemente no ponto [tex]\textcolor{#0000FF}{Lado_m}[/tex] e movimente-o.)
(4) A cada escolha de medida para os lados dos quadrados, o applet fornecerá a área de cada um deles e a soma dessas duas áreas.
OBMEP_ srdg, criado com o GeoGebra
Observamos que o applet ajuda na visualização da solução;
mas, matematicamente, não a substitui.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
