✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)
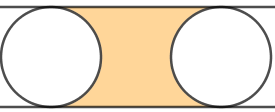
(UK Junior Mathematical Olympiad, 2015 – Adaptado) Dois círculos de raio [tex]2\,cm[/tex] tangenciam dois segmentos paralelos entre si, como mostrado na figura. Sabendo que a distância entre os centros desses círculos é [tex]6\,cm[/tex], determine a área da região colorida delimitada pelos círculos e pelos dois segmentos.

Lembrete
Toda reta tangente a uma circunferência é perpendicular ao raio no seu ponto de tangência.
Solução
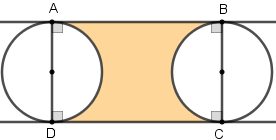
Sejam [tex]A[/tex], [tex]B[/tex], [tex]C[/tex] e [tex]D[/tex] os pontos de tangência que os dois segmentos determinam com relação às circunferências, conforme mostra a figura abaixo. Utilizando o Lembrete, podemos concluir que o quadrilátero [tex]ABCD[/tex] é um retângulo.
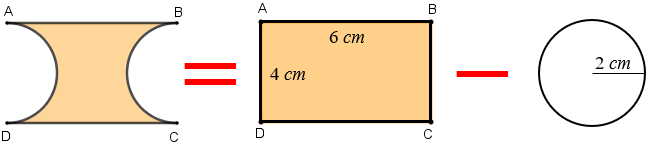
Observe que a área da região colorida delimitada pelos círculos e pelos dois segmentos é simplesmente a diferença entre a área do retângulo [tex]ABCD[/tex] e a área de dois semicírculos definidos pelos círculos de raio [tex]2\,cm[/tex] cada. Assim, a área da região colorida é a diferença entre a área do retângulo [tex]ABCD[/tex] e a área de um dos círculos da figura inicial.
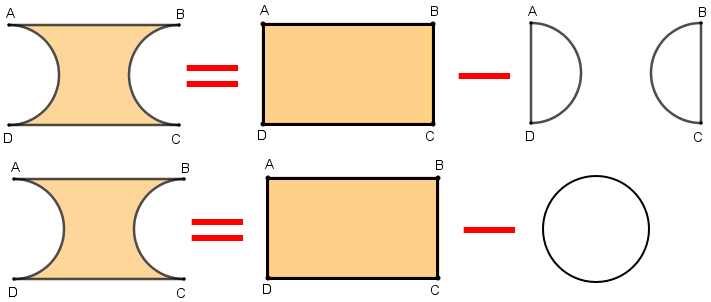
Perceba que, como os segmentos [tex]AD[/tex] e [tex]BC[/tex] são perpendiculares aos dois segmentos paralelos iniciais, então:
- o comprimento dos lados [tex]AB[/tex] e [tex]DC[/tex] do retângulo [tex]ABCD[/tex] é exatamente a distância entre os centros dos círculos.
- o comprimento dos lados [tex]AD[/tex] e [tex]BC[/tex] do retângulo [tex]ABCD[/tex] é exatamente o comprimento dos diâmetros desses círculos.
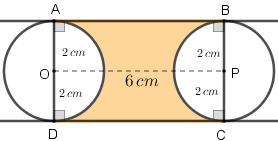
Vamos, então, aos cálculos da área colorida, que denotaremos por [tex]\textcolor{#FF9933}{A_{col}}[/tex]:
[tex]\qquad \qquad \textcolor{#FF9933}{A_{col}}=A_{ret}-A_{cir}[/tex]
[tex]\qquad \qquad \textcolor{#FF9933}{A_{col}}=6 \times 4-\pi \times 2^2[/tex]
[tex]\qquad \qquad \textcolor{#FF9933}{A_{col}}=24-4\pi[/tex]
[tex]\qquad \qquad \textcolor{#FF9933}{A_{col}}=4\left( 6-\pi \right)\,cm^2.[/tex]
Assim, a área da região colorida é, aproximadamente, [tex]\fcolorbox{black}{#fdb}{$11,43\, cm^2$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
