✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)
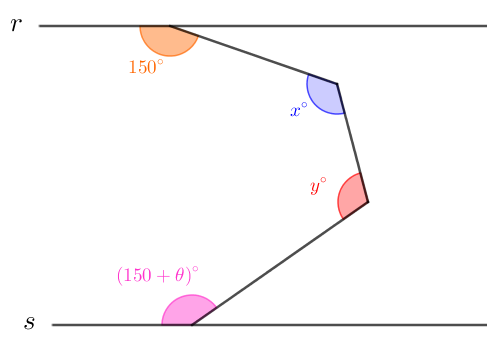
(ONEM, 2005 – Adaptado) As retas [tex]r[/tex] e [tex]s[/tex] da figura abaixo são paralelas e [tex]x^\circ+y^\circ=210^\circ[/tex].
Determine o valor de [tex]\theta[/tex].

Lembrete
A soma dos ângulos internos de um polígono convexo de [tex]n[/tex] lados [tex](n\gt 2)[/tex] é dada por:
[tex]\qquad \qquad \boxed{S_{n}=\left(n-2\right)\cdot 180^\circ}.[/tex]
Solução
A partir da figura fornecida no problema, tracemos a reta [tex]t[/tex] mostrada na imagem a seguir, de forma a definirmos um hexágono convexo. Denotaremos os vértices desse hexágono por [tex]A,\, B,\, C,\, D,\, E,\,F\,.[/tex]
Vamos passar a limpo o hexágono obtido, para facilitar a visualização da solução.
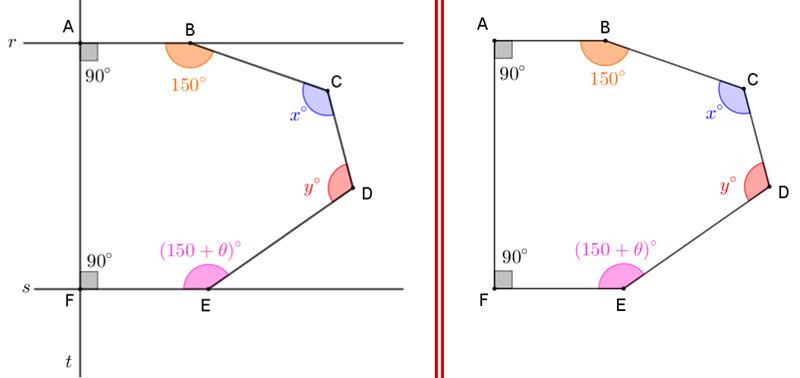
Utilizando o Lembrete, podemos concluir que a soma dos ângulos internos do hexágono [tex]ABCDEF[/tex] é
[tex]\qquad \qquad \left(6-2\right)\cdot 180^\circ=720^\circ[/tex],
então, segue que:
[tex]\qquad \qquad 90^\circ+150^\circ+x^\circ+y^\circ+\left(150^\circ+\theta\right)^\circ+90^\circ=720^\circ[/tex]
[tex]\qquad \qquad 480^\circ+x^\circ+y^\circ+\theta=720^\circ[/tex]
[tex]\qquad \qquad x^\circ+y^\circ+\theta=240^\circ[/tex].
Como, por hipótese, [tex]x^\circ+y^\circ=210^\circ[/tex], temos que:
[tex]\qquad \qquad 210^\circ+\theta=240^\circ[/tex]
[tex]\qquad \qquad \fcolorbox{black}{#eee0e5}{$\theta=30^\circ $}\,[/tex].
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
