✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)
(Extraído do livro Construindo Conhecimentos em matemática – Bianchini & Miani) No interior do quadrado [tex]ABCD[/tex], cujos lados têm comprimento [tex]10 \, cm[/tex], foram traçados dois quadrados e um retângulo, conforme indicado na figura.
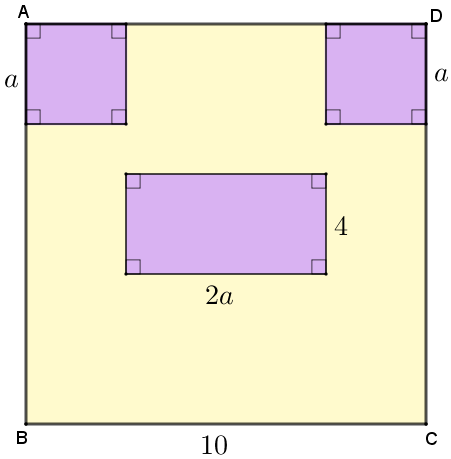
Sabendo que a área da região colorida de amarelo é [tex]58 \, cm^2 \, [/tex], determine o valor de [tex]a[/tex], em centímetros.
Solução
A área do quadrado de lado igual a [tex]10 \, cm[/tex] é [tex]100 \, cm^2[/tex] e, subtraindo dessa área total a área da região colorida de amarelo, obtém-se a área lilás. Assim, a área da região lilás é [tex]100-58= 42 \, cm^2[/tex].
Observamos que a soma das áreas pintadas de lilás é a soma das áreas de dois quadrados e de um retângulo; dessa forma, segue que:
[tex] \qquad a\cdot a + a\cdot a + 2a\cdot 4 = 42[/tex]
[tex] \qquad a^2 + a^2 + 8a = 42[/tex]
[tex] \qquad 2a^2 + 8a – 42 = 0 [/tex] (simplificando por [tex]2[/tex])
[tex] \qquad a^2 + 4a – 21 = 0.[/tex]
As raízes dessa equação de 2º grau são [tex]a_1=3[/tex] e [tex]a_2= -7[/tex], mas apenas a raiz [tex]a_1=3[/tex] satisfaz a condição de ser medida dos lados. Logo, segue que:
- o valor de [tex]a [/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$3 \, cm$} \, [/tex];
- a área de cada quadrado lilás é [tex]\boxed{ a\cdot a=9 \, cm^2}[/tex];
- a área do retângulo lilás é [tex]\boxed{ 2a\cdot 4= 24 \, cm^2}[/tex].
Solução elaborada pelo COM OCTETO MATEMÁTICO, com contribuições dos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
