✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Difícil)
O retângulo [tex]ABCD[/tex] da figura foi dividido em sete quadrados, de forma que cada um dos dois quadradinhos destacados tem perímetro [tex]4 \, cm[/tex].
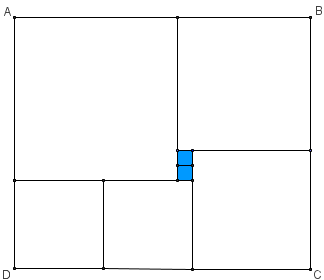
Qual o perímetro do retângulo [tex]ABCD[/tex] ?
Notação
Denotaremos o segmento definido por dois pontos, digamos [tex]X \, [/tex] e [tex] \, Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY[/tex].
Solução
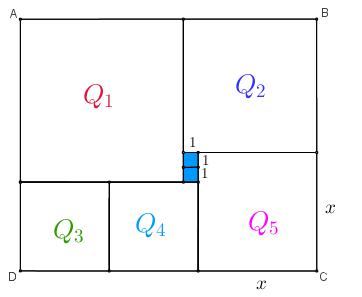
Como cada um dos dois quadradinhos coloridos em azul tem perímetro [tex]4 \, cm[/tex], os lados desses quadradinhos têm comprimento [tex]1 \, cm \, .[/tex]
- Suponhamos que os lados do quadrado inferior direito, [tex]Q_5[/tex], meçam [tex]x[/tex] centímetros, conforme mostra a próxima figura. Vamos encontrar os comprimentos dos lados dos demais quadrados, a partir de [tex]x \, .[/tex]
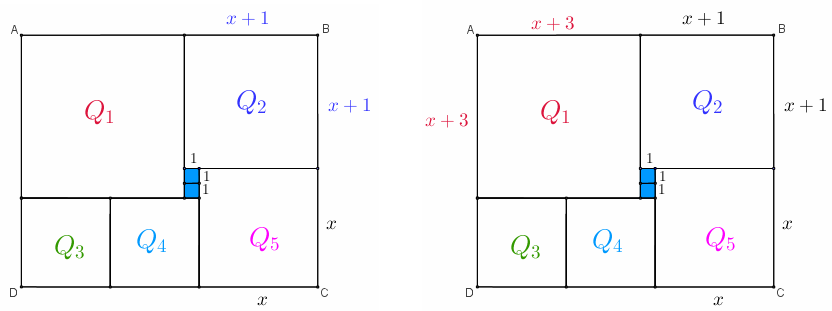
- A partir do lado de comprimento [tex]x[/tex], podemos observar que os lados do quadrado [tex]\textcolor{blue}{Q_2}[/tex] medem [tex]\textcolor{blue}{x+1}[/tex] centímetros e, a partir dos lados de [tex]\textcolor{blue}{Q_2}[/tex], observamos que os lados do quadrado [tex]\textcolor{#DC143C}{Q_1}[/tex] têm comprimentos [tex](x+1)+1+1=\textcolor{#DC143C}{x+3}[/tex] centímetros.
- Utilizando mais uma vez o comprimento [tex]x[/tex], concluímos que os lados do quadrado [tex]\textcolor{#0099FF}{Q_4}[/tex] medem [tex]\textcolor{#0099FF}{x-2}[/tex] centímetros, assim como os lados de [tex]\textcolor{#339900}{Q_3} \, .[/tex]
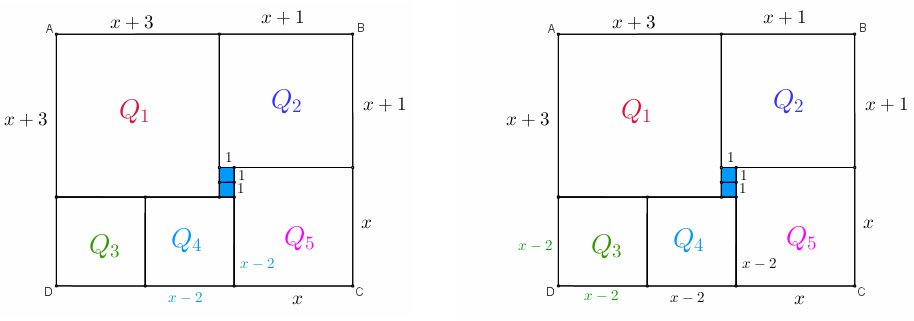
Podemos, agora, determinar o valor de [tex]x[/tex] e, consequentemente, o perímetro do retângulo [tex]ABCD[/tex].
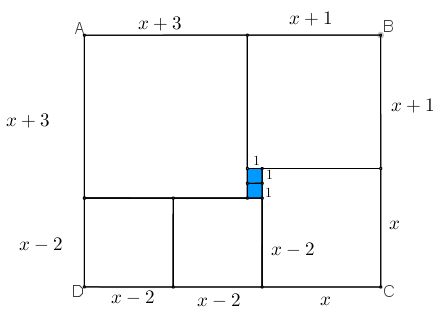
Observe que como [tex]ABCD[/tex] é um retângulo, então os lados [tex]\overline{AB}[/tex] e [tex]\overline{DC}[/tex] têm o mesmo comprimento; assim, segue que:
[tex]\qquad (x+3)+(x+1)=(x-2)+(x-2)+x[/tex]
[tex]\qquad 2x+4=3x-4[/tex]
[tex]\qquad \boxed{x=8 \, cm} \, .[/tex]
Dessa forma, temos as medidas dos lados de [tex]ABCD[/tex]:
- [tex]AB=(x+3)+(x+1)=8+3+8+1=20 \, cm[/tex]
- [tex]BC=(x+1)+x=8+1+8=17 \, cm[/tex]
e, finalmente, o perímetro do retângulo [tex]ABCD[/tex]: [tex] \, \, \fcolorbox{black}{#eee0e5}{$P=2\times(AB+BC)=2\times37=74 \, cm$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
