✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Fácil)
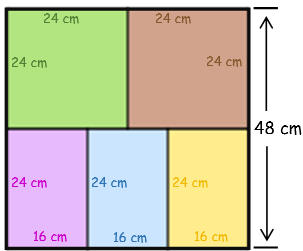
Dois quadrados e três retângulos foram utilizados para formar um quadrado maior, conforme mostra a figura.
Cada um dos dois quadrados menores tem [tex]96 \, cm[/tex] de perímetro e os três retângulos têm o mesmo tamanho.
Qual é o perímetro de cada retângulo?

Solução
Sabemos que o perímetro de um quadrado é quatro vezes o comprimento de cada lado. Assim:
- a medida dos lados dos quadrados menores é [tex]\dfrac{96}{4}=\boxed{24 \, cm} \, .[/tex]
Por outro lado, perceba que o comprimento dos lados do quadrado maior é duas vezes o comprimento dos lados de cada quadrado menor e três vezes o comprimento dos lados horizontais de cada retângulo. Portanto:
- o comprimento dos lados do quadrado maior é [tex]2 \times 24=\boxed{48 \, cm} \, [/tex],
- o comprimento dos lados horizontais de cada retângulo é [tex]\dfrac{48}{3}=\boxed{16 \, cm} \, .[/tex]
Finalmente, note que o comprimento dos lados verticais de cada retângulo é a diferença entre os comprimentos dos lados do quadrado maior e do quadrado menor ou, de outra forma, o mesmo comprimento dos lados dos quadrados menores. Dessa forma:
- o comprimento do lado vertical de cada retângulo é [tex]48-24=\boxed{24 \, cm} \, .[/tex]
Pelo exposto concluímos que o perímetro de cada retângulo que aparece na figura é igual a [tex]\boxed{2 \times 16 + 2 \times 24}= \fcolorbox{black}{#eee0e5}{$80 \, cm$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
