✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 6º ano do E. F. – Nível de dificuldade: Muito Difícil)
A bordo de um avião estavam [tex]201[/tex] pessoas de cinco nacionalidades diferentes. Sabe-se que, em cada grupo de seis dessas [tex]201[/tex] pessoas, pelo menos duas tinham a mesma idade.
Mostre que nesse avião viajaram, pelo menos, cinco passageiros de mesma nacionalidade, com a mesma idade e do mesmo sexo.
Solução
(1) Vamos, inicialmente, agrupar essas [tex]201[/tex] pessoas segundo suas nacionalidades.
Pelos dados do problema, teremos cinco grupos. Observe que existe pelo menos um grupo com no mínimo [tex]41[/tex] pessoas de mesma nacionalidade, já que, se todos os cinco grupos tivessem menos do que [tex]41[/tex] pessoas, então todos teriam no máximo [tex]40[/tex] pessoas e, assim, teríamos no máximo [tex]40 \times 5=200[/tex] pessoas no avião, o que contrariaria a informação de que a bordo estavam [tex]201[/tex] pessoas.
- Podemos então considerar um grupo N de [tex]41[/tex] pessoas com a mesma nacionalidade.
(2) Vamos agora agrupar as [tex]41[/tex] pessoas do grupo N segundo seu sexo: feminino ou masculino.
Perceba que existem pelo menos [tex]21[/tex] pessoas do mesmo sexo em N, pois se cada um desses dois novos grupos criados tivesse no máximo [tex]20[/tex] pessoas, no grupo N todo teríamos no máximo [tex]20 \times 2=40[/tex] pessoas e isso não é possível, pois esse grupo tem [tex]41[/tex] pessoas.
- Logo, podemos considerar um grupo NS de [tex]21[/tex] pessoas que têm a mesma nacionalidade e são do mesmo sexo.
(3) Agora, vamos dividir o grupo NS de acordo com as idades de seus componentes.
Observe que podemos dividir as [tex]21[/tex] pessoas desse grupo em, no máximo, cinco grupos de pessoas de mesma idade, pois se tivéssemos seis grupos teríamos seis pessoas com idades diferentes o que contrariaria a informação de que " em cada grupo de seis pessoas pelo menos duas tinham a mesma idade ". Dessa forma, podemos dividir as [tex]21[/tex] pessoas em, no máximo, cinco grupos.
Considerando esses cinco grupos percebemos que não é possível que todos tenham no máximo quatro pessoas; pois, se isso ocorresse, teríamos no máximo [tex]4\times 5=20[/tex] pessoas no grupo NS e sabemos que isso não ocorre.
- Assim, é possível extrair de NS um grupo NSI de, no mínimo, cinco pessoas com a mesma idade.
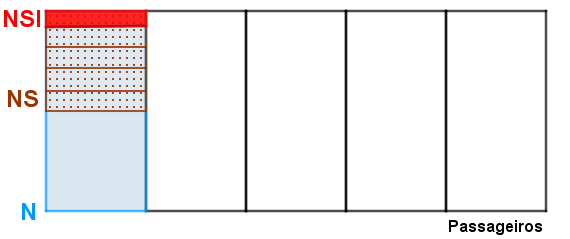
Lembrando que as pessoas do grupo NSI também têm a mesma nacionalidade e são do mesmo sexo, de fato, viajaram no avião pelo menos cinco passageiros de mesma nacionalidade, com a mesma idade e do mesmo sexo.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
