✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Médio)
Cláudia tem três filhos: Fábio, Felipe e Iuri.
Daqui a três anos, as idades de Iuri, Felipe e Fábio serão proporcionais a [tex]3[/tex], [tex]5[/tex] e [tex]7[/tex], nesta ordem.
Daqui a doze anos, as idades de Iuri, Felipe e Fábio serão proporcionais a [tex]3[/tex], [tex]4[/tex] e [tex]n[/tex], igualmente nesta ordem.
Determinar [tex]n[/tex].
Solução
Daqui a três anos, as idades de Iuri, Felipe e Fábio serão proporcionais a [tex]3[/tex], [tex]5[/tex] e [tex]7[/tex]; assim, existe [tex]k[/tex] tal que as três idades serão, respectivamente, [tex]3k[/tex], [tex]5k[/tex] e [tex]7k[/tex].
Dessa forma, podemos supor que:
- atualmente as idades de Iuri, Felipe e Fábio são, respectivamente, [tex]3k-3[/tex], [tex]5k-3[/tex] e [tex]7k-3 [/tex] ;
- dentro de doze anos, as idades de Iuri, Felipe e Fábio são, respectivamente, [tex](3k-3)+12[/tex], [tex](5k-3)+12[/tex] e [tex](7k-3)+12 .[/tex]
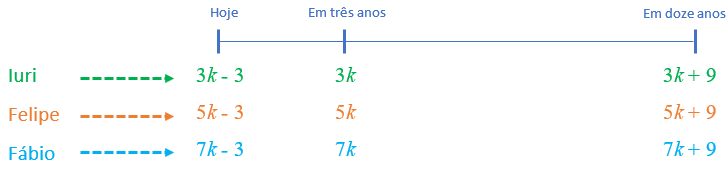
Mas temos a informação de que, daqui a doze anos, as idades de Iuri, Felipe e Fábio serão proporcionais a [tex]3[/tex], [tex]4[/tex] e [tex]n[/tex], nesta ordem; portanto, temos que:
[tex]\dfrac{(3k-3)+12}{3}=\dfrac{(5k-3)+12}{4}= \dfrac{(7k-3)+12}{n} .\qquad \qquad \textcolor{#800000}{(i)}[/tex]
Perceba que, da primeira igualdade, segue que:
[tex]\quad \dfrac{(3k-3)+12}{3}=\dfrac{(5k-3)+12}{4}[/tex]
[tex]\qquad \dfrac{3k+9}{3}=\dfrac{5k+9}{4}[/tex]
[tex]\qquad 12k+36=15k+27[/tex]
[tex]\qquad 3k=9[/tex]
[tex]\qquad \boxed{k=3}.[/tex]
Agora, substituindo [tex]k=3[/tex] em [tex]\textcolor{#800000}{(i)} [/tex] , segue que
[tex]\qquad \dfrac{18}{3}=\dfrac{24}{4}= \dfrac{30}{n} [/tex] ,
donde podemos concluir que [tex]\fcolorbox{black}{#eee0e5}{$n=5$}[/tex] .
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
