✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Fácil)
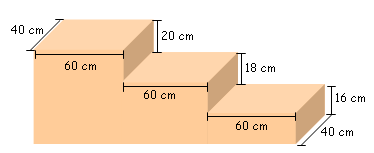
A partir de três blocos retangulares, o senhor João construiu um pódio para a premiação da maratona que será realizada na escola de seu filho.
Qual o volume do sólido resultante da construção?

Lembrete
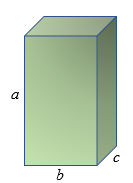
✐ O volume de um bloco retangular (ou paralelepípedo) cujos lados expressos na mesma unidade de comprimento medem [tex]a \, ; \, b \, ; \, c \, [/tex] é o produto dessas três medidas:
[tex]\qquad \qquad \boxed{V=a \cdot b \cdot c} \, .[/tex]
Solução
Observe que o pódio construído pelo “seu João” pode ser decomposto nos três blocos retangulares mostrados na figura a seguir.
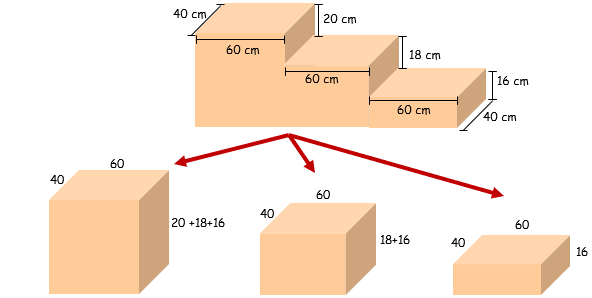
Dessa forma, o volume [tex]V[/tex] do pódio é a soma dos volumes dos três blocos mostrados na figura:
[tex]\qquad V=\overbrace{40\times 60\times (20+18+16)}^{V_1}+\overbrace{40\times 60\times (18+16)}^{V_2}+\overbrace{40\times 60\times 16}^{V_3}[/tex]
[tex]\qquad V=40\times 60\times \left[(20+18+16)+(18+16)+16\right][/tex]
[tex]\qquad V=40\times 60\times 104[/tex]
[tex]\qquad V=249 \, 600 \, cm^3[/tex].
Assim, o volume do pódio construído pelo “seu João” é [tex] \, \fcolorbox{black}{#eee0e5}{$249.600 \, cm^3$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
