✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F.) (Nível: Médio)
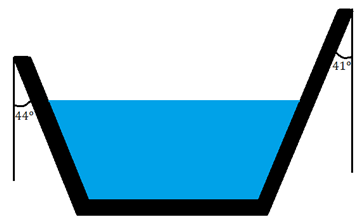
Um canal artificial que capta água de um certo rio possui seção transversal semelhante à da figura mostrada abaixo.
Se as paredes laterais do canal formam ângulos com as verticais conforme indicado, qual a medida em graus do ângulo definido pelo prolongamento das paredes laterais desse canal?
Solução
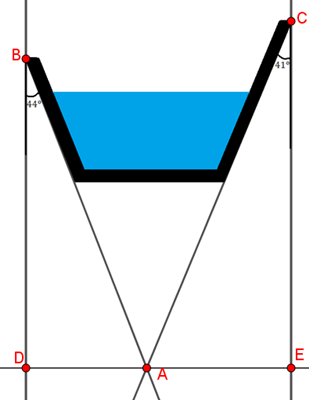
Observe, inicialmente, que os ângulos que as paredes laterais do canal formam com as paredes verticais não são congruentes (eles têm medidas diferentes); assim, as paredes laterais não são paralelas e seus prolongamentos na seção transversal do canal se intersectam em um ponto, digamos, [tex]A[/tex], conforme mostrado na figura abaixo. Nessa mesma figura, os pontos [tex]B[/tex] e [tex]C[/tex] são os vértices dos ângulos que as paredes laterais do canal formam com as verticais.
Consideraremos também os pontos [tex]D \, [/tex] e [tex] \, E[/tex], interseções da reta que passa por [tex]A[/tex] e é perpendicular às paredes verticais com cada parede vertical.
Dessa forma, podemos considerar os triângulos retângulos [tex]BDA[/tex] e [tex]CEA[/tex] mostrados na próxima figura, na qual representamos as medidas em graus dos ângulos [tex]B\hat{A}D[/tex], [tex]C\hat{A}E[/tex] e [tex]B\hat{A}C[/tex] por [tex]\alpha, \, \beta[/tex] e [tex]\theta[/tex], respectivamente.
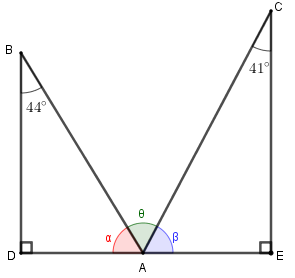
Vamos, então, calcular o valor de [tex]\theta[/tex].
Como os pontos [tex]D[/tex], [tex]A[/tex], [tex]E[/tex] são colineares, então
- [tex]\alpha+ \theta+\beta=180^\circ[/tex]. [tex]\qquad \textcolor{#800000} {(i)}[/tex]
Por outro lado, sabemos que a soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ[/tex]; e sendo [tex]BDA[/tex] e [tex]CEA[/tex] triângulos retângulos, segue que:
- [tex]\alpha+ 44^\circ+90^\circ=180^\circ[/tex]
[tex]\boxed{\alpha=46^\circ}[/tex], - [tex]\beta+90^\circ+41^\circ=180^\circ[/tex]
[tex]\boxed{\beta=49^\circ}[/tex].
Com esses valores, por [tex]\textcolor{#800000} {(i)}[/tex], temos que [tex]46^\circ+ \theta+49^\circ=180^\circ[/tex], ou seja, [tex]\theta=85^\circ[/tex].
Portanto, a medida do ângulo definido pelo prolongamento das paredes laterais do canal é [tex]85^\circ[/tex].
Uma segunda solução para este problema pode ser feita, se você sabe o que são ângulos alternos internos e que ângulos alternos internos são congruentes. Vejamos.
Considere, na seção transversal do canal, a reta vertical que passa pelo ponto [tex]A[/tex], interseção dos prolongamentos das paredes laterais, conforme mostrado na figura abaixo.
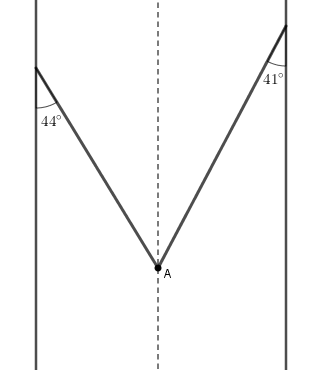
Perceba que, com as três retas paralelas, definimos os dois pares de ângulos alternos internos mostrados na próxima figura.
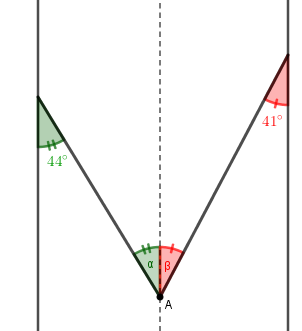
Perceba também que a medida [tex]\theta[/tex] do ângulo definido pelo prolongamento das paredes laterais do canal é a soma [tex]\alpha+\beta[/tex].
Assim, [tex]\boxed{\theta=\alpha+\beta=44^\circ+41^\circ=85^\circ}[/tex].
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
