✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
Uma pequena empresa fabrica um produto que tem um preço de venda de R$ 20,00.
Se o preço de custo de cada unidade desse produto é R$ 11,00 e a empresa tem custos fixos mensais de R$ 8.000,00 para a produção, determine o número mínimo de unidades do produto que a empresa deve vender por mês para que comece a ter lucro com a venda.
Solução
Seja [tex]n[/tex] o número mínimo de unidades do produto em questão que a empresa deve vender por mês para que comece a ter lucro com a venda. Observe que:
- o preço em reais de venda dessas [tex]n[/tex] unidades do produto é [tex] \, V= 20n \, [/tex];
- o preço em reais do custo de produção dessas [tex]n[/tex] unidades do produto é [tex] \, C= 11n+8000 \, .[/tex]
Assim, o possível lucro da empresa com a venda dessas [tex]n[/tex] unidades será:
[tex]\qquad L= V-C[/tex]
[tex]\qquad L=20n-\left(11n+8000\right)[/tex]
[tex]\qquad L=9n-8000.[/tex]
Portanto, para que a empresa comece a ter lucro devemos ter [tex]L \gt 0[/tex] e, assim:
[tex]\qquad 9n-8000 \gt 0[/tex]
[tex]\qquad 9n \gt 8000[/tex]
[tex]\qquad n \gt \dfrac{8000}{9}\approx 888,89 \, [/tex].
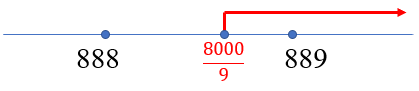
Como [tex]n[/tex] é uma quantidade de unidades de um produto, então [tex]n[/tex] deve ser um número natural e, dessa forma, devemos ter [tex]\fcolorbox{black}{#eee0e5}{$n=889$}.[/tex]
Com isso, a empresa deve vender, no mínimo, [tex]889[/tex] unidades do produto por mês, para começar a ter lucro com a venda.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
