.Problema para ajudar na escola: Expressão máxima

Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Difícil)

(ONEM, 2008) Seja $ABC$ um triângulo tal que $AB= 3\, \text{cm}$ , $\,BC=5\, \text{cm}\,$ e $\, CA=4\, \text{cm}$ .
Se $P$ é um ponto do plano determinado pelos vértices desse triângulo, qual o valor máximo da expressão
$\qquad \qquad \boxed{2\left(PB\right)^2-\left(PA\right)^2-3\left(PC\right)^2}$ ?

Notação: Se $X$ e $Y$ são pontos de um plano, estamos indicando por $XY$ a distância entre esses dois pontos.

Solução

Vamos transformar esse problema geométrico em um problema algébrico, já que a expressão $\boxed{2\left(PB\right)^2-\left(PA\right)^2-3\left(PC\right)^2}$ que vamos majorar não está associada a alguma forma geométrica conhecida.
Veja no vídeo disponibilizado abaixo que transformar problemas geométricos em problemas algébricos é a essência da chamada Geometria Analítica e faremos isso definindo um sistema cartesiano conveniente, a partir do triângulo $ABC$ definido no problema.
Observe que $3^2+4^2=5^2$; assim, o triângulo $ABC$ é um triângulo retângulo.
Considere, então,

• o sistema cartesiano $xAy$, com origem no ponto $A$ e cujos eixos horizontal e vertical são definidos respectivamente pelos vértices "$A$ e $C$" e "$A$ e $B$", de modo que os pontos $B$ e $C$ tenham coordenadas $\boxed{B=(0,3)}\,$ e $\,\boxed{C=(4,0)}\,.$ Observe que neste sistema $\,\boxed{A=(0,0)}\,.$

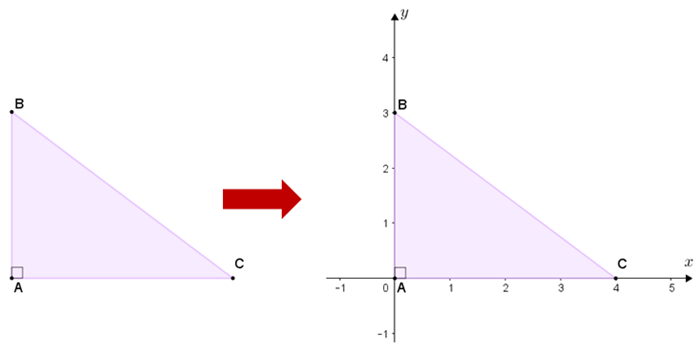
Suponha que as coordenadas do ponto $P$ no nosso sistema referencial de coordenadas sejam $P=(x,y)$.
Como a distância $d$ entre dois pontos cujas coordenadas com relação a um mesmo plano cartesiano são $\left(x_1,y_1\right)\,$ e $\,\left(x_2,y_2\right)$ é dada por
$\qquad \qquad d=\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}$,
e as medidas $PA$, $PB$ e $PC$ são simplesmente as distâncias de "$P$ a $A$", de "$P$ a $B$" e de "$P$ a $C$", respectivamente, temos que:

• $PA=\sqrt{\left(x-0\right)^2+\left(y-0\right)^2}=\sqrt{x^2+y^2}$;
• $PB=\sqrt{\left(x-0\right)^2+\left(y-3\right)^2}=\sqrt{x^2+\left(y-3\right)^2}$;
• $PC=\sqrt{\left(x-4\right)^2+\left(y-0\right)^2}=\sqrt{\left(x-4\right)^2+y^2}$.

Com isso, podemos escrever algebricamente a expressão a ser majorada da seguinte forma:
$\qquad \boxed{2\left(PB\right)^2-\left(PA\right)^2-3\left(PC\right)^2}=\\ \qquad =2 \left(\sqrt{x^2+\left(y-3\right)^2}\right)^2-\left(\sqrt{x^2+y^2}\right)^2-3\left(\sqrt{\left(x-4\right)^2+y^2}\right)^2\\ \qquad =2 \left(x^2+y^2-6y+9\right)-\left(x^2+y^2\right)-3\left(x^2-8x+16+y^2\right)\\ \qquad =-2x^2-2y^2+24x-12y-30\\ \qquad =-2\left(x^2-12x\right)-2\left(y^2+6y\right)-30\,.$
Para facilitar a análise da expressão, vamos fazer dois processos de completamento de quadrado.(Se você não se lembra desse procedimento, dê uma passadinha nesta Sala de Leitura.). Observe:
$\qquad \boxed{2\left(PB\right)^2-\left(PA\right)^2-3\left(PC\right)^2}=\\ \qquad =-2\left[\left(x^2-12x+36\right)-36\right]-2\left[\left(y^2+6y+9\right)-9\right]-30\\ \qquad =-2\left(x-6\right)^2+72-2\left(y+3\right)^2+18-30\\ \qquad =-2\left(x-6\right)^2-2\left(y+3\right)^2+60\\ \qquad =\boxed{-2\left[\left(x-6\right)^2+\left(y+3\right)^2\right]+60}\,.$
Finalmente, observe que $\left(x-6\right)^2+\left(y+3\right)^2 \geqslant 0$; assim, segue que:
$\qquad -2\left[\left(x-6\right)^2+\left(y+3\right)^2\right] \leqslant 0\\ \qquad -2\left[\left(x-6\right)^2+\left(y+3\right)^2\right]+60 \leqslant 60\\ \qquad \boxed{2\left(PB\right)^2-\left(PA\right)^2-3\left(PC\right)^2} \textcolor{red}{\leqslant} 60 \,.$

Dessa forma, o maior valor assumido pela expressão $\boxed{2\left(PB\right)^2-\left(PA\right)^2-3\left(PC\right)^2}$ é $\fcolorbox{black}{#eee0e5}{$60$}\,.$
Uma informação complementar:
Veja que a expressão $\boxed{2\left(PB\right)^2-\left(PA\right)^2-3\left(PC\right)^2}$ assume o valor $60$ somente quando $\left(x-6\right)^2+\left(y+3\right)^2 = 0$ e, neste caso, temos $x=6$ e $y=-3$.
Dessa forma, o maior valor da expressão $\boxed{2\left(PB\right)^2-\left(PA\right)^2-3\left(PC\right)^2}$ ocorre quando o ponto $P$ tem coordenadas $(6,-3)\,.$
Você pode verificar essa informação utilizando o applet disponibilizado a seguir.

Solução elaborada pelos Moderadores do Blog.