.Problema para ajudar na escola: Esporte preferido

Problema
(A partir do 8º ano do E. F.) (Nível: médio)

---

O professor de Educação Física de uma escola fez uma enquete com alguns alunos sobre o esporte preferido por cada um.
Os dados dessa pesquisa foram apresentados em um gráfico de setores:

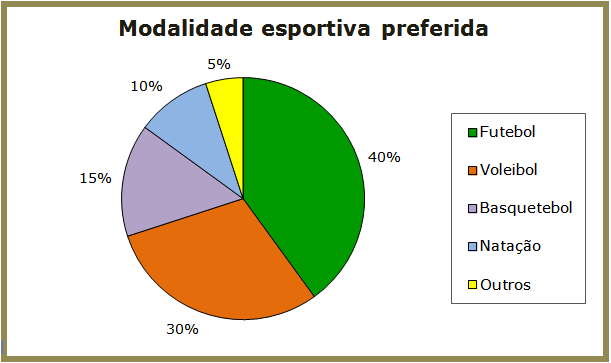
Sabendo que 75 entrevistados têm o basquetebol como o esporte preferido, pergunta-se:
(a) Quantos entrevistados preferem o futebol?
(b) Quantos entrevistados preferem o voleibol?
(c) Quantos alunos foram entrevistados?

Ferramentas que ajudam

---

Informações numéricas podem ser veiculadas de diversas formas. Ao folhearmos jornais e revistas, por exemplo, encontramos informações numéricas não só em textos, mas também em tabelas e gráficos.
Particularmente, os gráficos constituem uma forma clara e objetiva de expressar visualmente dados numéricos; com eles é possível, em um pequeno espaço, visualizar um grande número de informações. Para o nosso dia a dia, essa visualização rápida e objetiva facilita a leitura, a interpretação e a utilização de informações numéricas importantes.
Existem vários tipos de gráficos: a utilização de cada um depende do tipo de análise que se pretende com a apresentação das informações numéricas que se tem em mãos. Dentre os mais utilizados estão os gráficos de colunas, de barras, de setores e de linha.

Solução 1

---

Para resolver o problema, vamos estabelecer proporções entre “o total de alunos entrevistados” (o todo) e “as preferências por cada esporte” (as partes).

• Começaremos relacionando o todo com a parte que se refere aos alunos entrevistados que têm o basquetebol como o esporte preferido, já que essa é a única categoria para a qual temos a quantidade de alunos e sua respectiva porcentagem do todo: se os [tex]75[/tex] alunos que preferem o basquetebol correspondem a [tex]15\%[/tex], quantos alunos correspondem a [tex]100\%[/tex] dos entrevistados?
  Denotaremos essa quantidade de alunos por [tex]x[/tex] e para estabelecer a proporção utilizaremos uma regrinha de três simples:

[tex]x[/tex] alunos	————————————–	[tex]100\%[/tex]
[tex]75[/tex] alunos	————————————–	[tex]15\%[/tex]

Dessa forma, obtemos que [tex]100\times 75= 15x[/tex], donde [tex]x=\dfrac{7500}{15}=500[/tex].

Este total de [tex]500[/tex] alunos entrevistados não só responde ao item (c), como também ajuda na solução dos itens (a) e (b).

• Observando o gráfico, percebemos que [tex]40\%[/tex] dos entrevistados preferem o futebol. Dentre os [tex]500[/tex] alunos entrevistados, quantos alunos correspondem a [tex]40\%[/tex]?
  Denotaremos essa quantidade de alunos por [tex]f[/tex] e para estabelecer a proporção utilizaremos outra regra de três simples:

[tex]500[/tex] alunos	————————————–	[tex]100\%[/tex]
[tex]f[/tex] alunos	————————————–	[tex]40\%[/tex]

Assim, obtemos que [tex]500\times 40= 100f[/tex], donde [tex]f=\dfrac{20000}{100}=200[/tex].

• Quantos alunos correspondem aos [tex]30\%[/tex] dos entrevistados que o gráfico aponta que preferem o voleibol?
  Essa quantidade de alunos será denotada por [tex]v[/tex]; logo:

[tex]500[/tex] alunos	————————————–	[tex]100\%[/tex]
[tex]v[/tex] alunos	————————————–	[tex]30\%[/tex]

Assim, obtemos que [tex]500\times 30= 100v[/tex], donde [tex]v=\dfrac{15000}{100}=150[/tex].

Portanto:
(a) [tex]200[/tex] alunos preferem o futebol.

(b) [tex]150[/tex] alunos preferem o voleibol.

(c) Foram entrevistados [tex]500[/tex] alunos.

---

Solução elaborada pelos Moderadores do Blog.

Solução 2

---

Seja N o total de alunos.
Sabemos que 15% de N é 75, então é correto dizer que 1% de N é 5.
Como 1% de N é 5, então:
a) Se o número de alunos que gostam de futebol é 40% de N, temos 40*5 = 200 alunos.

b) Se o número de alunos que gostam de voleibol é 30% de N, temos 30*5 = 150 alunos

c) Se o total é 100% de N, temos 100*5 = 500 alunos.

---

Solução elaborada pelo Clube Matemáticos do Érico.

Solução 3

---

Sabemos que [tex]75[/tex] entrevistados têm o basquete como esporte favorito, o que corresponde a [tex]15\%[/tex] do total de entrevistados. Desse modo, considerando o total de entrevistados como [tex]x[/tex], temos que:

[tex]\qquad \dfrac{15}{100}\cdot{x} = 75[/tex]

[tex]\qquad \dfrac{15x}{100} = 75[/tex]

[tex]\qquad 15x = 75\cdot100[/tex]

[tex]\qquad 15x = 7500[/tex]

[tex]\qquad x = \dfrac{7500}{15}[/tex]

[tex]\qquad x = 500[/tex]

Sabendo que [tex]x = 500[/tex], podemos resolver os outros itens:

a) [tex]\dfrac{40}{100}\cdot500 = \dfrac{200\cancel{0}\cancel{0}}{1\cancel{0}\cancel{0}} = 200[/tex] entrevistados preferem futebol.

b) [tex]\dfrac{30}{100}\cdot500 = \dfrac{150\cancel{0}\cancel{0}}{1\cancel{0}\cancel{0}} = 150[/tex] entrevistados preferem voleibol.

c) Como visto anteriormente, foram entrevistados [tex]500[/tex] alunos.

---

Solução elaborada pelo Clube 1uik.