✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 3ª série do E. M.- Nível de dificuldade: Fácil)
Um soldador abriu duas latas cilíndricas idênticas paralelamente aos seus eixos (linhas tracejadas, na figura) e as soldou para formar uma lata maior.
Qual a relação entre o volume de cada lata menor e o volume da lata maior?
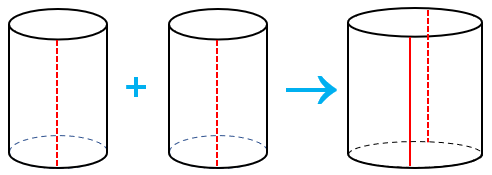
Adaptado de Canguru de Matemática Brasil, 2014.
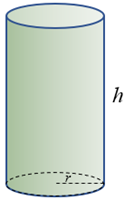
Lembrete
✐ Volume de um cilindro circular reto cujo comprimento da altura é [tex]h[/tex] e o comprimento do raio da base é [tex]r[/tex]:
[tex]\qquad \qquad \boxed{Volume=\pi\,r^2 h}.[/tex]
Solução
O esquema abaixo mostra as etapas da transformação das duas latas menores na lata maior. Observe que as três latas envolvidas no processo têm a mesma altura.
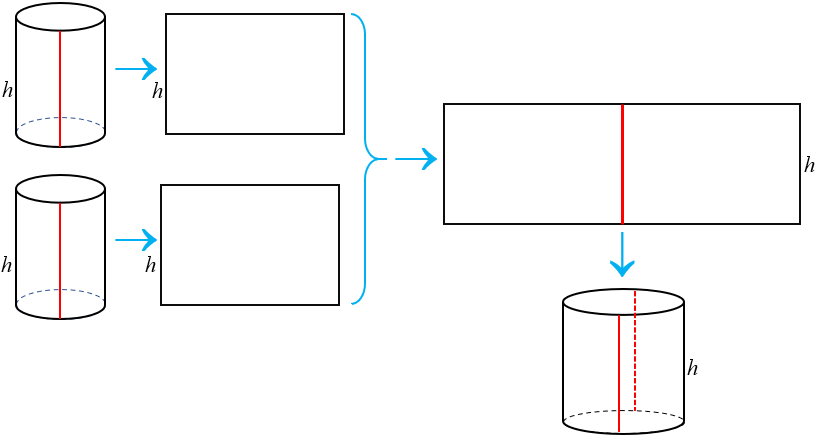
Vamos comparar os volumes das latas e cada lata é um cilindro circular reto; como já temos as respectivas alturas, precisaremos determinar as respectivas "áreas da base" dos cilindros. Para isso, vamos observar os retângulos que aparecem no processo ilustrado acima.
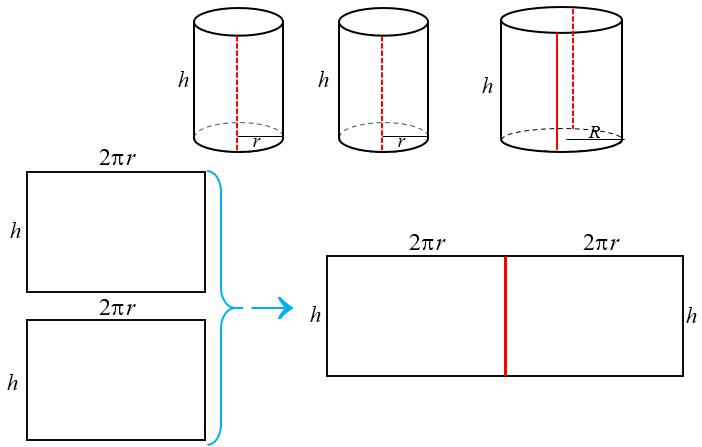
Perceba que os comprimentos das bases dos dois retângulos menores nos quais foram transformadas as duas latas menores equivalem aos perímetros das circunferências que definem as bases dos cilindros menores. Analogamente, o comprimento da base do retângulo maior é o perímetro da circunferência que define a base do cilindro maior.
Então, se [tex]r[/tex] e [tex]R[/tex] são os raios das bases do cilindro menor e do cilindro maior, respectivamente, [tex]2\pi r[/tex] é o perímetro da base de cada cilindro menor e [tex]2\pi R[/tex] é o perímetro da base do cilindro maior.
Assim, [tex]2\pi R=4\pi r[/tex], donde [tex]R=2r[/tex].
Finalmente, se [tex]V_m[/tex] é o volume de cada lata menor e [tex]V_M[/tex] é o volume da lata maior, então segue que:
[tex]\qquad \dfrac{V_m}{V_M}=\dfrac{\pi r^2 h}{\pi R^2 h}\\
\qquad \dfrac{V_m}{V_M}=\dfrac{\cancel{\pi} r^2 \bcancel{h}}{\cancel{\pi} R^2 \bcancel{h}}\\
\qquad \dfrac{V_m}{V_M}=\dfrac{r^2 }{R^2 }\\
\qquad \dfrac{V_m}{V_M}=\dfrac{r^2 }{\left(2r\right)^2 }\\
\qquad \dfrac{V_m}{V_M}=\dfrac{r^2 }{4r^2 }\\
\qquad \dfrac{V_m}{V_M}=\dfrac{\cancel{r^2} }{4\cancel{r^2 }}\\
\qquad \dfrac{V_m}{V_M}=\dfrac{1 }{4}\\
\qquad \fcolorbox{black}{#eee0e5}{$V_M=4V_m$}\,.[/tex]
Portanto, o volume da lata maior é quatro vezes o volume da lata menor.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
