✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Fácil)
Durante uma viagem, a velocidade de um carro varia, conforme as condições da estrada e as condições meteorológicas.
O gráfico abaixo mostra a velocidade do carro do meu irmão, a cada instante, na última viagem que ele fez para a casa da minha mãe.
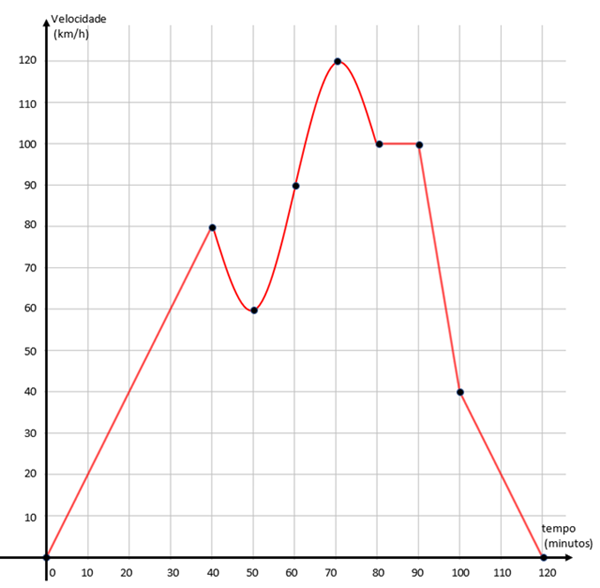
(a) Qual a velocidade do carro do meu irmão após uma hora de viagem?
(b) Em que momentos da viagem a velocidade do carro foi [tex]40\, km/h[/tex]?
(c) Qual a velocidade máxima alcançada ao longo do trajeto? Em que momento ela foi atingida?
(d) Qual a velocidade máxima alcançada durante a primeira hora da viagem? Em que momento isso aconteceu?
(e) Qual a velocidade mínima alcançada no intervalo de tempo “a partir da primeira meia hora e até uma hora e meia” de percurso? Em que instante isso aconteceu?
(f) Em algum trecho do trajeto a velocidade foi constante?
(g) Em que intervalos de tempo a velocidade aumentou e em que intervalos ela diminuiu?
Solução
Observe inicialmente que temos um gráfico cujo eixo horizontal nos fornece os tempos decorridos, em minutos, e cujo eixo vertical nos dá a velocidade do carro em cada momento, em quilômetros por hora, durante as duas horas de uma viagem. Perceba que a velocidade do carro é função do tempo ([tex]v=f(t)[/tex]); logo, para cada tempo corresponde uma única velocidade, mas uma mesma velocidade pode corresponder a tempos de viagem distintos.
Vamos às respostas:
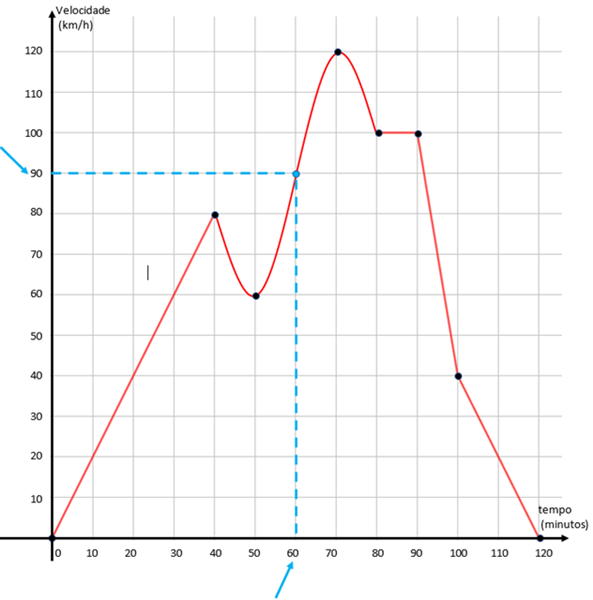
(a) A velocidade do carro após uma hora de viagem é a velocidade correspondente a [tex]t=60[/tex], já que uma hora equivale a [tex]60[/tex] minutos.
Observando no gráfico, a velocidade que corresponde a [tex]t=60\, min[/tex] é [tex]v=90\, km/h\, .[/tex]
Assim, a velocidade do carro do meu irmão exatamente após uma hora de viagem foi de [tex]\fcolorbox{black}{#eee0e5}{$90\, km/h$}.[/tex]
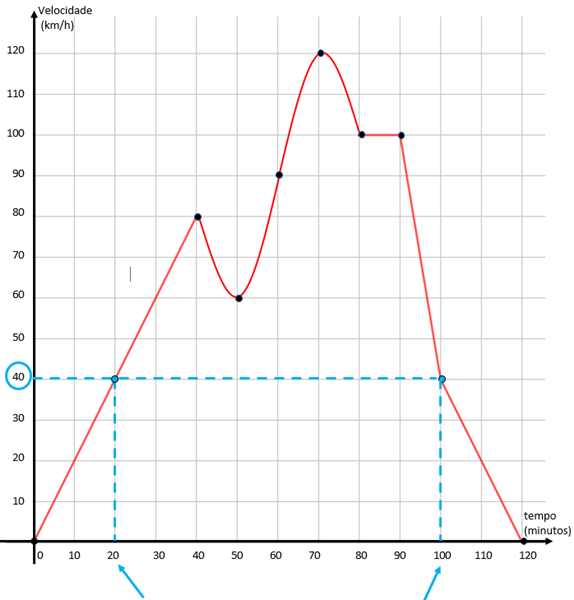
(b) A partir do ponto que corresponde a [tex]v=40[/tex] no eixo vertical, traçamos uma reta horizontal e identificamos por quais pontos do gráfico essa reta passa. Em seguida, observamos que esses pontos correspondem aos valores [tex]t=20\, min[/tex] e [tex]t=100\, min[/tex] do eixo horizontal.
Consequentemente, a velocidade do carro foi [tex]40\, km/h[/tex] em dois momentos da viagem: ao fim de [tex]\fcolorbox{black}{#eee0e5}{$20 \text{ minutos}$}[/tex] e ao fim de [tex]\fcolorbox{black}{#eee0e5}{$ 100 \text{ minutos }$}.[/tex]
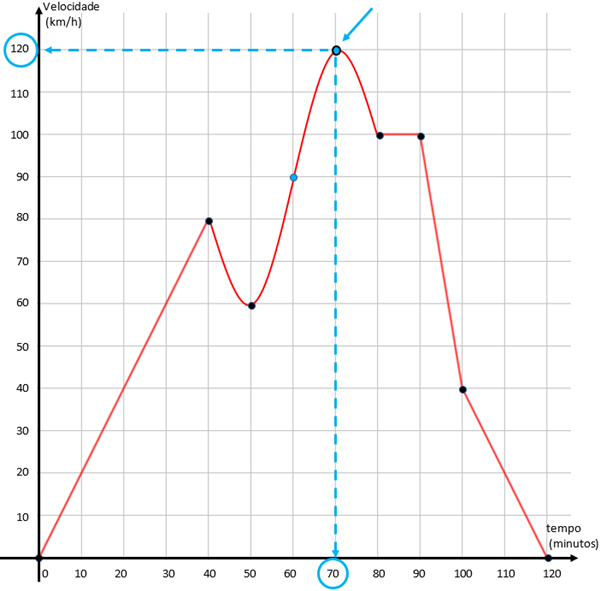
(c) Observe que o ponto “mais alto” do gráfico que nos foi apresentado é aquele que corresponde ao maior valor do eixo vertical e, portanto, representa a maior velocidade alcançada pelo carro durante as duas horas de viagem.
No caso, essa velocidade foi de [tex]\fcolorbox{black}{#eee0e5}{$120\, km/h$}[/tex] e ela foi atingida aos [tex]\fcolorbox{black}{#eee0e5}{$70$}[/tex] minutos da viagem.
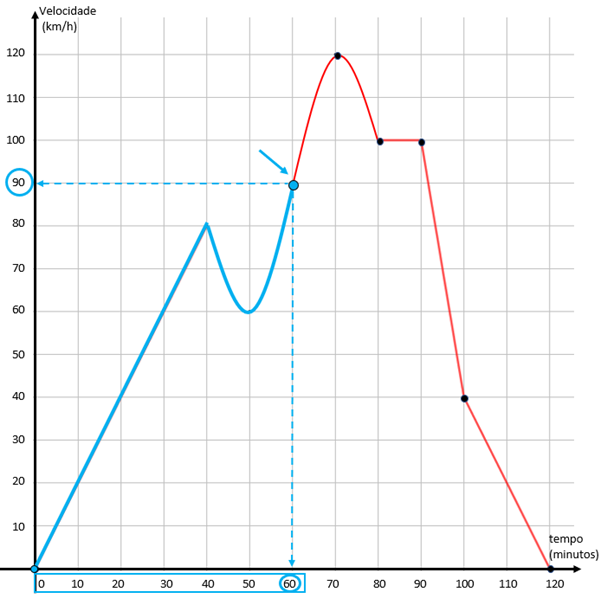
(d) Neste item consideraremos os dados relativos aos primeiros [tex]60[/tex] minutos de viagem, já que precisaremos calcular a velocidade máxima alcançada durante a primeira hora da viagem e em que instante(s) essa velocidade foi alcançada.
Para isso, nos limitaremos a analisar o gráfico no intervalo de [tex]0[/tex] a [tex]60[/tex] minutos, incluindo os extremos [tex]0[/tex] e [tex]60[/tex] minutos. Note, agora que, nesse intervalo, o ponto “mais alto” do gráfico, e aquele que nos dá maior velocidade alcançada, é o ponto correspondente a [tex]t=60\, min\, [/tex] e [tex]v=90\, km/h .[/tex]
Assim, a velocidade máxima durante a primeira hora da viagem foi [tex]\fcolorbox{black}{#eee0e5}{$90\, km/h$}[/tex] e ela foi atingida exatamente aos [tex]\fcolorbox{black}{#eee0e5}{$60$}[/tex] minutos, ou seja, ao final da primeira hora.
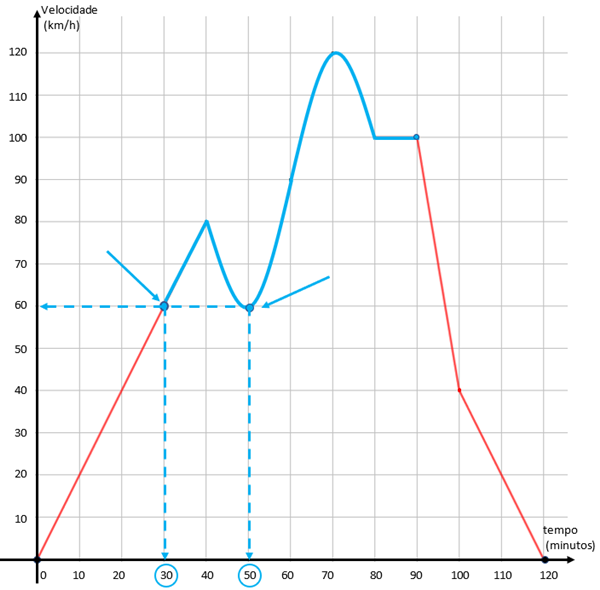
(e) Vamos considerar para este item os dados relativos ao intervalo de [tex]30[/tex] a [tex]90[/tex] minutos, incluindo os extremos [tex]30[/tex] e [tex]90[/tex], e vamos focar no(s) ponto(s) mais baixo(s) do gráfico para esse intervalo de tempo, uma vez que queremos a velocidade mínima, que é aquela que corresponde ao menor valor do eixo vertical relativo ao intervalo.
Observando o gráfico dado na questão, percebemos que são dois os pontos mais baixos considerando o intervalo em questão. Esses pontos indicam [tex]v=60\, km/h[/tex] como a velocidade mínima do intervalo e [tex]t=30\, min[/tex] e [tex]t=50\, min[/tex] como os tempos correspondentes a essa velocidade.
Pelo exposto, a velocidade mínima alcançada no intervalo de tempo “a partir da primeira meia hora e até uma hora e meia” de percurso foi de [tex]\fcolorbox{black}{#eee0e5}{$60\, km/h$}[/tex] e foi atingida em dois momentos: aos [tex]\fcolorbox{black}{#eee0e5}{$30$}[/tex] e aos [tex]\fcolorbox{black}{#eee0e5}{$50$}[/tex] minutos da viagem.
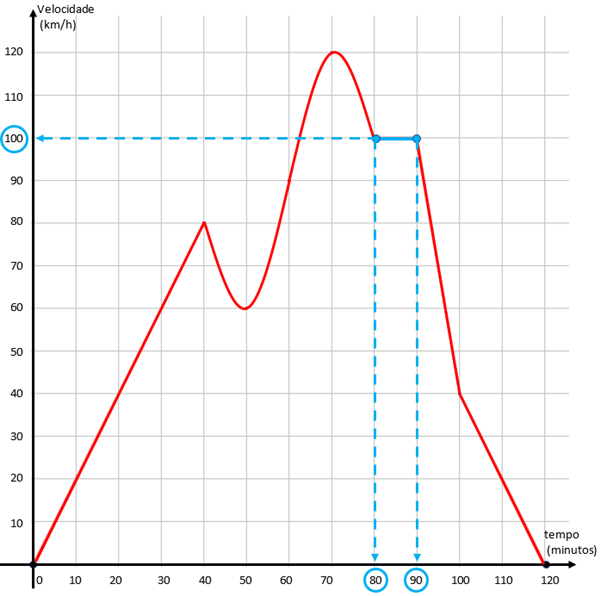
(f) Se em algum trecho do trajeto a velocidade do carro foi constante, isso significa graficamente que, no intervalo de tempo que o carro percorreu esse trecho, o gráfico é um segmento de reta horizontal, uma vez que a velocidade é a mesma em todo o intervalo.
Observando o gráfico, verificamos que no intervalo de [tex]80[/tex] a [tex]90[/tex] minutos a velocidade do carro se manteve em [tex]100\, km/h.[/tex]
Com isso, concluímos que no trecho do trajeto percorrido pelo carro entre [tex]\fcolorbox{black}{#eee0e5}{$\text{ 80 e 90 minutos }$}[/tex] a velocidade foi constante (e somente nesse intervalo).
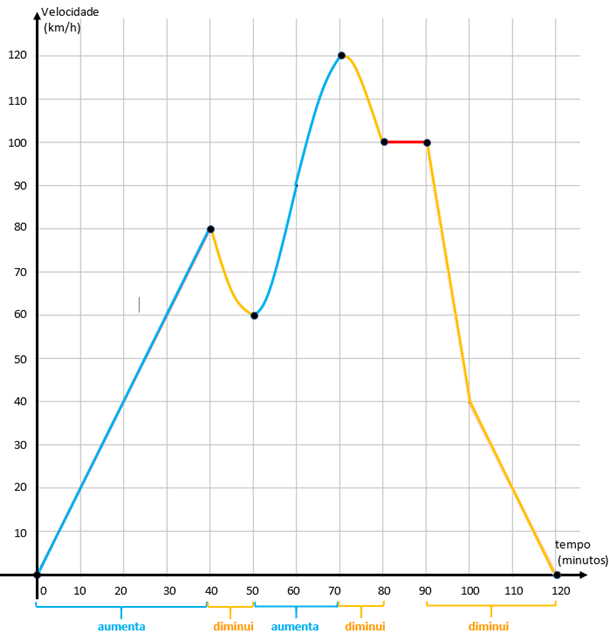
(g) Vamos ver o que acontece com a velocidade durante as duas horas do trajeto.
- Observe que no início do trajeto a velocidade é zero e vai aumentando, conforme aumenta o tempo, até os [tex]40[/tex] minutos iniciais da viagem.
- Exatamente aos [tex]40[/tex] minutos de viagem a velocidade é de [tex]80\, km/h[/tex] e nesse instante a velocidade começa a diminuir até que aos [tex]50[/tex] minutos atinge [tex]60\, km/h[/tex] e volta a aumentar.
- Aumenta em todo o intervalo de [tex]50[/tex] a [tex]70[/tex] minutos e aos [tex]70[/tex] minutos a velocidade já é [tex]120\, km/h[/tex].
- A partir dos [tex]70[/tex] minutos de viagem, a velocidade diminui até atingir os [tex]100\, km/h[/tex] aos [tex]80[/tex] minutos.
- Permanece constante por dez minutos e volta a diminuir a partir dos [tex]90[/tex] minutos e assim prossegue até o término da viagem.
Concluímos então que:
- a velocidade aumentou do início da viagem até os [tex]40[/tex] minutos, voltando a crescer no intervalo de [tex]50[/tex] a [tex]70[/tex] minutos;
- a velocidade diminuiu no intervalo de [tex]40[/tex] a [tex]50[/tex] minutos, voltando a diminuir no intervalo de [tex]70[/tex] a [tex]80[/tex] minutos e diminui mais uma vez a partir dos [tex]90[/tex] minutos e até o final da viagem, aos [tex]120[/tex] minutos.
Solução elaborada pelos Moderadores do Blog.