✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
Quatro crianças estão em diferentes pontos do contorno de um parquinho com forma circular.
Esse parquinho tem uma torneira com água potável e uma das quatro crianças está a [tex]2[/tex] metros do local dessa torneira, outra está a [tex]4[/tex] metros do mesmo local e uma terceira está a [tex]10[/tex] metros, conforme ilustra a figura abaixo.
Qual a distância entre a criança que está no ponto B e o local da torneira?
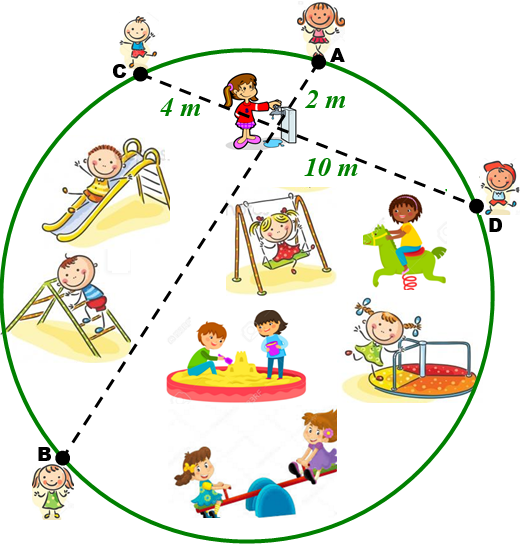
Imagens extraídas de "http://www.smartkids.com.br/" e "https://pt.depositphotos.com/portfolio-3827765.html".

Ajuda
Este problema pode ser facilmente resolvido, se você conhece a relação métrica relativa a uma circunferência conhecida como Cruzamento entre duas cordas. Essa propriedade garante que se duas cordas de uma circunferência se intersectam, então o produto entre as medidas das duas partes de uma corda é igual ao produto das medidas das duas partes da outra corda.
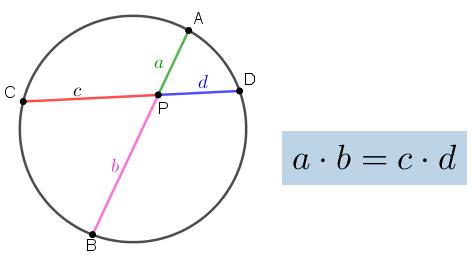
Solução 1
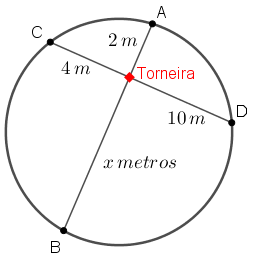
Seja [tex]x[/tex] a distância entre a criança que está no ponto B e o local da torneira.
Assim, pela propriedade explicitada na Ajuda, segue que:
[tex]\qquad 2x=4\times 10 [/tex]
[tex]\qquad 2x=40[/tex]
[tex]\qquad x=20[/tex]
Portanto, a distância entre a criança que está no ponto B e o local da torneira
é de [tex] \, \fcolorbox{black}{#eee0e5}{$20 \, m$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Se você não conhece a propriedade explicitada na Ajuda mas conhece a relação entre ângulo inscrito e seu respectivo ângulo central, também é possível resolver o problema.
Sendo [tex]T[/tex] o ponto no qual está a torneira, observe os triângulos [tex]ATD[/tex] e [tex] \, CTB[/tex] e perceba que:
- os ângulos [tex]A\hat{T}D[/tex] e [tex] \, C\hat{T}B[/tex] são OPV (opostos pelo vértice), logo são congruentes (têm a mesma medida).
- os ângulos [tex]B\hat{C}D[/tex] e [tex] \, B\hat{A}D \, [/tex] “enxergam” o mesmo arco [tex]\stackrel{\textstyle\frown}{\mathrm{BD}}[/tex], assim o ângulo central a eles associados é o mesmo e portanto ambos têm a mesma medida: [tex]\dfrac{\text{medida do ângulo central}}{2}[/tex], ou seja, são também congruentes.
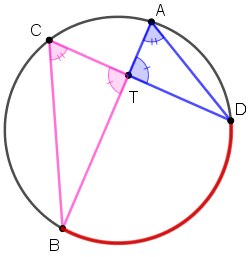

Dessa forma, vemos que os triângulos [tex]ATD[/tex] e [tex] \, CTB[/tex] são semelhantes e, portanto, têm lados correspondentes proporcionais.
Segue, então, que:
[tex]\qquad \dfrac{4}{2}=\dfrac{x}{10} [/tex]
[tex]\qquad 2x=4\times 10 [/tex]
[tex]\qquad 2x=40[/tex]
[tex]\qquad x=20[/tex]
Portanto, a distância entre a criança que está no ponto B e o local da torneira
é de [tex] \, \fcolorbox{black}{#eee0e5}{$20 \, m$} \, .[/tex]
Sugestão: Você pode utilizar a argumentação desta segunda solução para mostrar a validade da propriedade da AJUDA.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
