.Problema para ajudar na escola: Coração tem perímetro? E área?

Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)

O coração mostrado nas figuras foi desenhado em uma malha quadriculada, utilizando-se quatro arcos de circunferências: $\stackrel{\textstyle\frown}{\mathrm{AB}}$ , $\stackrel{\textstyle\frown}{\mathrm{BC}}$ , $\stackrel{\textstyle\frown}{\mathrm{CD}}$ , $\stackrel{\textstyle\frown}{\mathrm{DA}}$, cujos centros estão indicados por pontos azuis na forma de cruz.

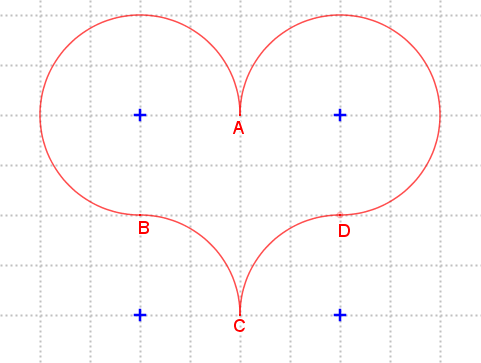
Sabendo-se que os lados dos quadradinhos da malha medem $1 \, \text{cm}$, determine:

(a) O perímetro do coração.

(b) A área do coração.

Solução

(a) Observe as circunferências de centros nos pontos $C_1, \, C_2, \, C_3, \, C_4$, a partir das quais foram traçados os arcos $\stackrel{\textstyle\frown}{\mathrm{AB}}$ , $\stackrel{\textstyle\frown}{\mathrm{BC}}$ , $\stackrel{\textstyle\frown}{\mathrm{CD}}$ , $\stackrel{\textstyle\frown}{\mathrm{DA}}$ que definem o coração.

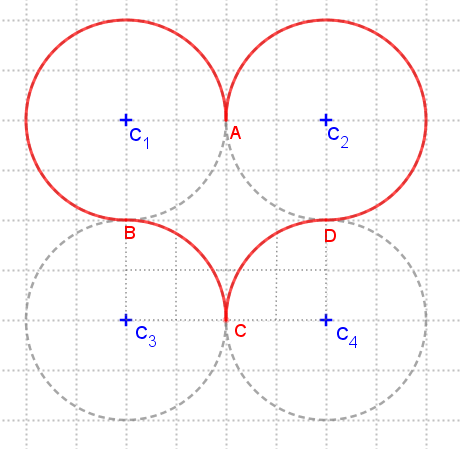
Note que cada uma dessas circunferências tem raio $r=2 \, \text{cm}$; logo, cada uma tem perímetro $\boxed{p=2\pi \, r=4\pi \, \text{cm}} \, .$
Se denotarmos o perímetro do coração por $\textcolor{red}{p_{cor}}$, segue que:
$\qquad \textcolor{red}{p_{cor}}=\dfrac{3}{4}p+\dfrac{1}{4}p+\dfrac{1}{4}p+\dfrac{3}{4}p$

$\qquad \textcolor{red}{p_{cor}}=\dfrac{8}{4}p$
$\qquad \textcolor{red}{p_{cor}}=2p$
$\qquad \textcolor{red}{p_{cor}}=2\times(4\pi)$
$\qquad \textcolor{red}{p_{cor}}=8\pi.$
Assim, o perímetro do coração é $\, \fcolorbox{black}{#eee0e5}{$8\pi \, \text{cm}$} \, .$ Se utilizarmos $3,14$ como aproximação para $\pi$, o perímetro do coração será aproximadamente $25,12 \, \text{cm}.$

(b) A área do coração corresponde à soma das áreas $A_1, \, A_2, \, A_3$ indicadas na figura abaixo: $\boxed{\textcolor{red}{A_{cor}}=A_1+A_2+A_3}.$

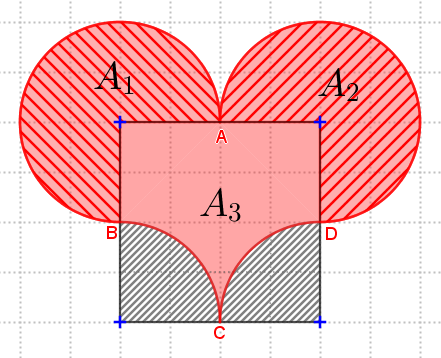
Observe que:

• Cada uma das áreas $A_1$ e $A_2$ corresponde à área de $\frac{3}{4}$ de um círculo de raio $r=2 \, \text{cm}$. Assim:

$\qquad A_1=A_2=\dfrac{3}{4}\pi \, r^2$

$\qquad A_1=A_2=\dfrac{3}{4}\pi \, 2^2$

$\qquad A_1=A_2=\dfrac{3}{\cancel{4}}\pi \, \cancel{4}$

$\qquad \boxed{A_1=A_2=3\pi \, \text{cm}^2}.$

• A área $A_3$ corresponde à diferença entre a área de um quadrado de lado $l=4 \, \text{cm}$ e duas áreas de $\frac{1}{4}$ de um círculo de raio $r=2 \, \text{cm}$. Logo:

$\qquad A_3=l^2-2\times \dfrac{1}{4}\pi \, r^2$

$\qquad A_3=4^2-2\times \dfrac{1}{4}\pi \, 2^2$

$\qquad A_3=16-2\times \dfrac{1}{\cancel{4}}\pi \, \cancel{4}$

$\qquad \boxed{A_3=(16-2\pi )\, \, \text{cm}^2}.$

Dessa forma,
$\qquad \textcolor{red}{A_{cor}}=A_1+A_2+A_3$
$\qquad \textcolor{red}{A_{cor}}=3\pi+3\pi+16-2\pi$
$\qquad \textcolor{red}{A_{cor}}=4\pi+16 \, .$
Portanto, a área do coração é $\, \fcolorbox{black}{#eee0e5}{$(4\pi+16) \, \text{cm}^2$} \,$. Se utilizarmos $3,14$ como aproximação para $\pi$, a área do coração é aproximadamente$28,56 \, \text{cm}^2.$

Solução elaborada pelos Moderadores do Blog.