✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
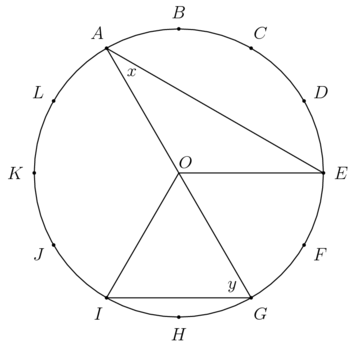
Uma circunferência foi dividida em [tex]12[/tex] arcos de mesma medida, como na figura.
Quantos graus tem o ângulo descrito pela diferença entre [tex]y[/tex] e [tex]x[/tex]?

Lembretes
✐ Uma das maneiras de se resolver este problema é utilizarmos a relação entre ângulo central e ângulo inscrito:
- Fixada uma circunferência, a medida de um ângulo inscrito é a metade da medida do ângulo central correspondente.
Caso você tenha perdido a discussão que fizemos sobre esse assunto no nosso Blog, clique AQUI.
✐ Para uma segunda solução, basta lembrar que:
- Os ângulos da base de um triângulo isósceles têm a mesma medida. (Se precisar, veja o finalzinho desta página.)
- A soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex]. (Se precisar, visite esta página.)
Solução 1
Como a circunferência foi dividida em [tex]12[/tex] arcos de mesma medida, a medida angular de cada arco é [tex]\dfrac{120^{\circ}}{12}=30^{\circ}[/tex]. Assim:
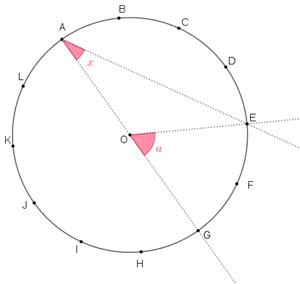
- a medida do ângulo central [tex]E\hat{O}G[/tex] é [tex]a=60^{\circ}[/tex] e, dessa forma, a medida [tex]x[/tex] do ângulo inscrito [tex]E\hat{A}G[/tex] é [tex]\fcolorbox{black}{#eee0e5}{$x=\dfrac{60^{\circ}}{2}=30^{\circ}$} \, .[/tex]
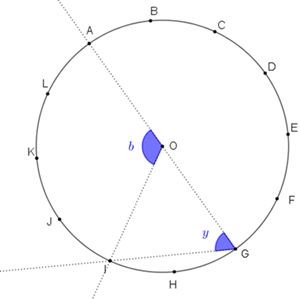
- a medida do ângulo central [tex]A\hat{O}I[/tex] é [tex]b=120^{\circ}[/tex]; logo, a medida [tex]y[/tex] do ângulo inscrito [tex]A\hat{G}I[/tex] é [tex]\fcolorbox{black}{#c4c4ff}{$y=\dfrac{120^{\circ}}{2}=60^{\circ}$} \, .[/tex]
Dessa forma, [tex]\boxed{y-x=60^{\circ}-30^{\circ}=30^{\circ}} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
A circunferência foi dividida em [tex]12[/tex] arcos de mesma medida, logo a medida angular de cada arco é [tex]\dfrac{120^{\circ}}{12}=30^{\circ}[/tex]. Assim:
- a medida do ângulo central [tex]E\hat{O}A[/tex] é [tex]120^{\circ}[/tex];
- a medida do ângulo central [tex]I\hat{O}G[/tex] é [tex]60^{\circ}[/tex].
Perceba, agora, que os triângulos [tex]EOA[/tex] e [tex]GOI[/tex] são isósceles, logo os respectivos ângulos da base de cada um têm a mesma medida. Com isso, como a soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex], então:
[tex]\textcolor{#800000}{(i)}[/tex] [tex]2x+120^{\circ}=180^{\circ}[/tex], donde [tex]\fcolorbox{black}{#eee0e5}{$x=30^{\circ}$} \, .[/tex]
[tex]\textcolor{#800000}{(ii)}[/tex] [tex]2y+60^{\circ}=180^{\circ}[/tex], donde [tex]\fcolorbox{black}{#c4c4ff}{$y=60^{\circ}$} \, .[/tex]
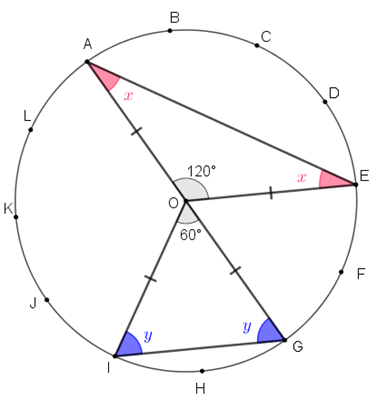
Igualmente obtemos [tex]\boxed{y-x=60^{\circ}-30^{\circ}=30^{\circ}} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
